[题目链接 - Codeforces Round 931 (Div. 2)](https://codeforces.com/contest/1934)
A. Too Min Too Max
题意
给出一个数组, 现在要你选择四个下标 , 问 最大是多少。( 必须互不相同)
思路
题目要求的其实就是选出四个数组成一个环,使得相邻两个数的差的和最大。
于是我们先探究 : 如果选出了某四个数,如何调整他们在环中的顺序能使得总和最大。 不难想到, 将较大的两个数放在第一和第三位, 较小的两个数放在第二和第四位时, 得到的结果最大。 此时为( ,即
第二步我们考虑如何选择这四个数能使得结果最大。 很明显我们需要尽可能让 较大的两个数 更大,较小的两个数更小。
于是对于整个数组,选出最大的两个数,以及最小的两个数,就可以得到最优结果。
对数组a进行排序, 就得到了最终结果为
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| #include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
void solve(){
int n;
cin>>n;
vector<int> a;
rep(i,1,n){int num;cin>>num;a.push_back(num);}
sort(a.begin(),a.end());
cout<<2*(a[n-1]+a[n-2]-a[0]-a[1])<<'\n';
}
signed main(){
int T = 1;
cin>>T;
while(T--){
solve();
}
return 0;
}
|
B. Yet Another Coin Problem
题意
现在有一些面值为 的硬币 , 问如何选择各个硬币的数量,使得总面值恰好为n,并且硬币的总数量最少。
undefined1 \le n \le 10^9)$
思路
我们观察这些硬币的面值,可以发现 都是3的倍数。而另一个大面值硬币又可以表示为 。于是我们有如下策略:
- 尽可能多地选择3 ,此时可能剩下的面值。即 , 如果md 为0,那么我们就可以将这些面值为3的硬币尽可能多地兑换为面值为15和6的硬币。
如果有剩余, 若手中面值3的硬币的数量大于等于3 ,就可以将这三个3和一个1 换成一个10。
如果有剩余并且手中的面值3的硬币数量小于3,那么就只能用面值为1的硬币来填补这个空缺了。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| #include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
void solve(){
int n;
cin>>n;
int md = n%3;
int t = n/3;
int ans = 0;
if(md == 2){
if(t>=3) {ans++;t-=3;}
else ans++;
md = 1;
}
if(md == 1){
if(t >= 3) {ans++;t-=3;}
else ans++;
md = 0;
}
ans += t / 5;
t %= 5;
ans += t / 2;
t %= 2;
ans+=t;
cout<<ans<<'\n';
}
signed main(){
int T = 1;
cin>>T;
while(T--){
solve();
}
return 0;
}
|
C. Find a Mine
题意
和上一场的C一样,又是交互题。 给出一个n *m的网格,其中有两个位置有地雷,但你不知道他们在哪, 你最多可以询问四次。
每次提供一个坐标, 裁判会告诉你两个地雷距离这个坐标的**曼哈顿距离** 中的最小值是多少。 现在需要你在最多四次询问之后,给出任意一颗地雷的具体坐标。
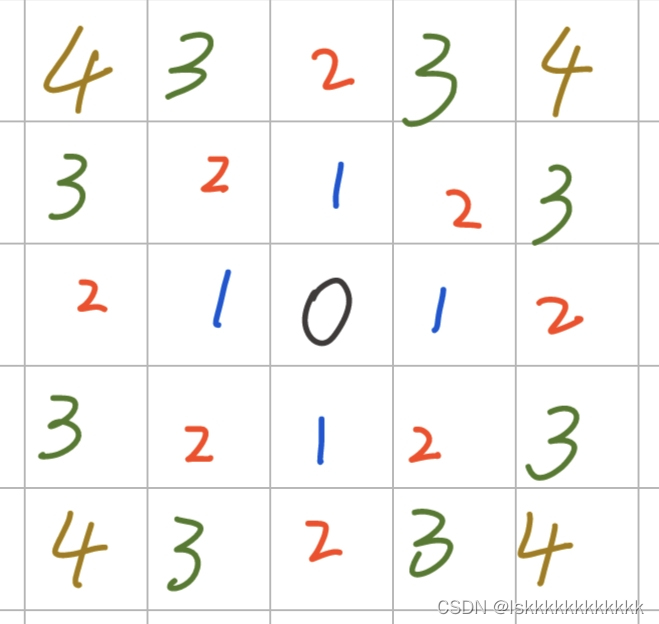
**曼哈顿距离** : 两个坐标undefinedx1 ,y1) , (x2,y2)|x1-x2|+|y1-y2|(3,3)$与所有点的曼哈顿距离如下
思路
我们发现确定一个点以及一个曼哈顿距离后 ,我们可以得到可能的范围是一个菱形。 如果我们将询问点设置在表格的一角,那么表格中可能的格子就组成了一个对角线。 于是我们询问地图的三个角,就得到了三条对角线,他们三者相交一定最多次出现两个交点。(也可能是一个)。之后我们再询问其中一个交点,如果给出的答案是0,就代表他是地雷,如果不是0,就代表另一个是地雷。
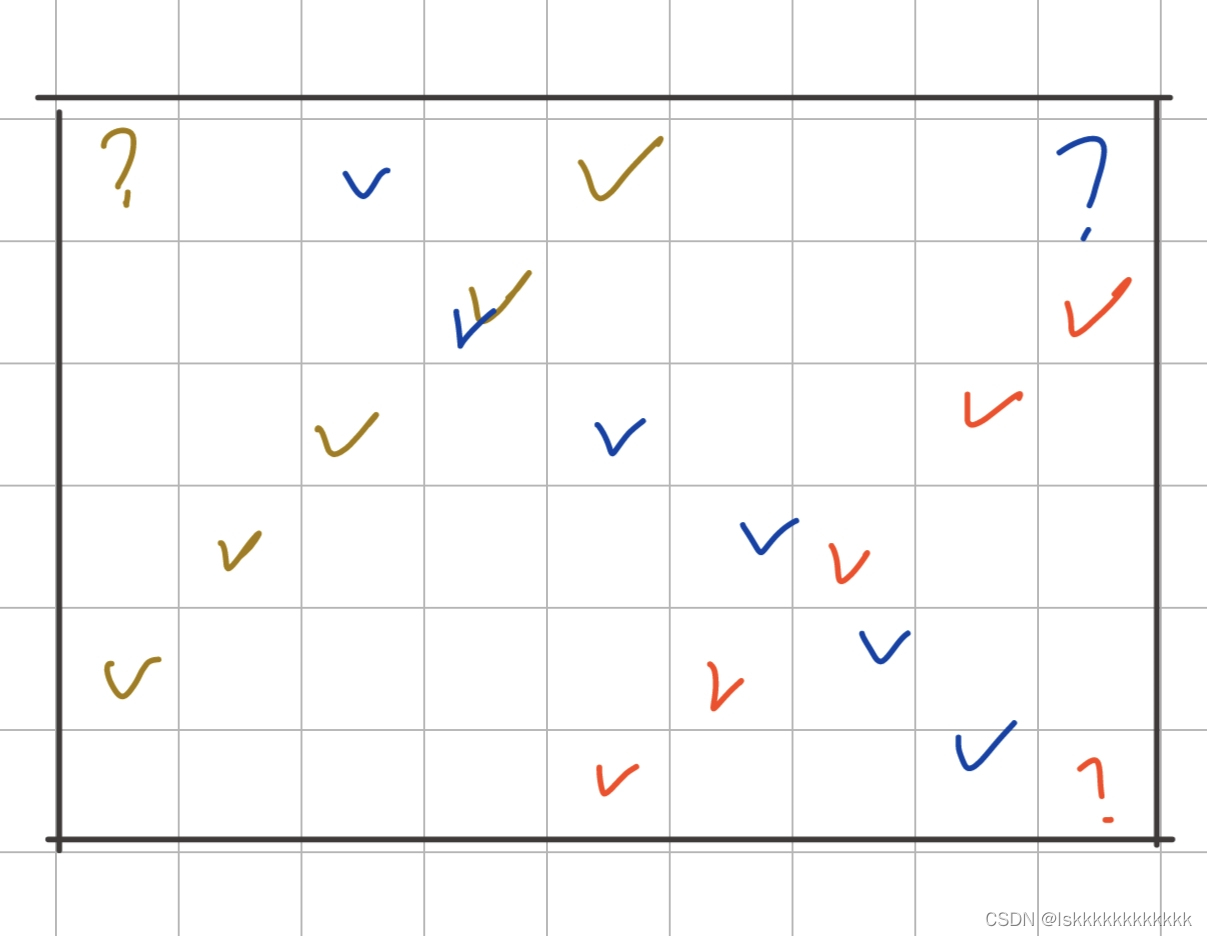
我们可能遇到两个对角线相交没有准确格子的情况(如上图中的红对角线和蓝对角线,二者没有共同的格子)
代码
这里有些地方需要讲解一下:
在代码中,先询问了左上,右下,右上三个角。得到了三个曼哈顿距离 。
怎么求两个交点呢? 先看左上和右上两个对角线形成的交点。假设为undefinedx_1,y_1)$ ,那么就有
解方程可以得到 , 但我们发现可能会出现x和y不是整数的时候(也就是为偶数的时候),这时候就不可取。(代码中表示为将x和y都设置为-1)
按照同样的方法
可以找到另一个交点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| #include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
int n,m;
bool inrange(int x,int y){
if(x<=n && x >= 1 && 1<=y && y<=m) return true;
else return false;
}
void solve(){
cin>>n>>m;
cout<<"? 1 1"<<endl;
int a; cin>>a;
cout<<"? "<<n<<" "<<m<<endl;
int b;cin>>b;
cout<<"? 1 "<<m<<endl;
int c;cin>>c;
int x1,y1,x2,y2;
int t = a+c - (m-1);
if(t%2){x1 = y1 = -1;}
else {y1 = t/2+1;x1 = (a-t/2)+1;}
t = b+c - (n-1);
if(t%2){x2 = y2 = -1;}
else{y2 = m-t/2;x2=(c-t/2)+1;}
if(!inrange(x1,y1)) {cout<<"! "<<x2<<" "<<y2<<endl;}
else if(!inrange(x2,y2)) {cout<<"! "<<x1<<" "<<y1<<endl;}
else{
cout<<"? "<<x1<<" "<<y1<<endl;
int d;cin>>d;
if(d == 0) cout<<"! "<<x1<<" "<<y1<<endl;
else cout<<"! "<<x2<<" "<<y2<<endl;
}
}
signed main(){
int T = 1;
cin>>T;
while(T--){
solve();
}
return 0;
}
|
D1. XOR Break — Solo Version
题意
给出操作方法为:若操作前的数值为,那么选择一个x ,使得 , 之后令或 。
给出n和mundefinedm<n)$ 问能否让n进行一定次数的操作后, 变为m。
undefinedoplusx \oplus y xy$的异或 。
思路
首先应该注意到的是: 我们不论选择还是 ,都是等价的,因为若令 那么不妨将我们设置的原先的更改为 这样选择 是等价的。 因此我们对于某个y,他可以一步变化的数为集合undefined{x| x<n\& x\oplus y < y \}$
接下来我们可以发现如下两个规律:
- 如果是11111(全1),那么y可以变为任意小于的数。
- 如果= 10000(只有一个1),那么y再也不能变化了 。
接下来我们找对于n所形成的可达的集合。其中的最大值:
先找到n的前两个为1的位置。(如果n只有一个1那么根据规律2可知无解),假设为a和b,如
当 时, 。(从左往右标注从1开始的下标)
那么为了使得和都比小,二者必须有一个变成0。
并且此时得知一个引论: 在a和b中间的这部分数位,m中的该部分必须全为0 。(反例:n = 101000,m = 01000,这里在m的第2位为1于是n一定不能到达m) ,否则便无解。
于是新的n(我们将他命名为)则是 或者 。我们发现对于b右边的数位(也就是第二个1之后的数位),无论他如何改变,都可以满足nn^n 和nn均小于n(因为最靠前的两个1位已经保证了这个性质),那么我们不妨让之后的数位都变为1(因为这样子可以尽可能地满足规律1,使得到更有可能)
于是我们得到如下结论,在令一个原本为1的位置变为0后,如果n中已经出现过至少两个1,那么之后的数位都可以变为1 。
那么应该把哪一位的1变为0呢?
检查n和m的二进制数,然后从大端找,找第一个n和m数位不同的地方,这时候一定是n的数位是1,m的数位是0
比如
发现左边第二位是1,于是将这一位置为0 , 这样就保证了对于前两位的1,有 m 和n^m都小于n。在此之后,将之后的位置(第3位到第6位)都变为1,便得到了nn = 101111 。我们构造的这个保证了在前半部分和m完全相同,无需理会,后半部分又全是1,可以随意变换。也就是说,只要nn大于m,那么一定可以从变成。
因此我们得知了变化顺序 ,由于可能等于,因此也可能是 。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| #include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
void solve(){
int n,m;
cin>>n>>m;
int nn = n;
int flag = 0;
for(int i = 62;i>=0;i--){
if(flag == 0 && ((n>>i)&1)!=((m>>i)&1)){
flag = 1;
nn -= (1<<i);
}
else if(flag == 1 && (n>>i)&1==0){
flag = 2;
}else if(flag == 2){
nn |= (1<<i);
}
}
if(nn<m){cout<<-1<<endl;return;}
if(nn == m){
cout<<2<<endl;
cout<<n<<" "<<m<<endl;
}else{
cout<<3<<endl;
cout<<n<<" "<<nn<<" "<<m<<endl;
}
}
signed main(){
int T = 1;
cin>>T;
while(T--){
solve();
}
return 0;
}
|
