强化学习数学原理笔记
可能会出现公式加载错误的情况,可以直接下载pdf版本。
强化学习数学原理
第一章基本概念
grid-world example : 一个机器人走网格的经典例子,机器人尽量避免进入forbidden grid、尽量减少拐弯、不要走出边界、……
state: 状态,表示为一个节点,在grid-world中可以表示为一个格子(也可以添加其他信息到状态,如速度等)
state space:状态空间,所有状态的集合。
action:行动,能够使得状态变化的动作。(如向上/下/左/右移动,等)
action space:行动的集合,通常依赖于当前的状态。
state transition:状态转移,从一个状态移动到另一个状态。
$s_5 \overset{a_1}{\rightarrow} s_6$ 表示从状态$s_5$ 经过动作$a_1$ 到达状态 $a_6$
state transition probability: 状态转移的条件概率。(例如:$p(s_2|s_1,a_2) = 0.8$ 代表在状态$s_1$,行动$a_2$ 下,$s_2$的概率是0.8)
Policy: 策略,用箭头来表示。表示在某个状态更倾向于走哪个action
$\pi(a1|s_1)=0 ,\pi(a_2|s_1)=1,\pi(a_3|s_1)=0 ,\pi(a_4|s_1)=0$ 表示在状态$s_1$ 有1的概率进行行动$a_2$ 。显然$\sum{i=1}^k \pi(a_i|s_1) = 1$
reward: 他是一个实数,代表我们的奖励,如果$reward>0$,则代表希望它发生,$reward<0$则表示不希望它发生。
例如我们可以将“尝试逃出边界的时候,我们设$r{bound} = -1$ , 将到达目的地设为$r{target} = 1$
因此我们可以通过设计reward来实现到达目的地。
$p(r=-1|s_1,a_1) = 1, p(r \not= -1 |s_1,a_1)=0$ 表示在状态$s_1$ 进行$a_1$ 得到-1的reward的概率是1,得到不是-1的reward的概率是0
trajectory:一个由state、action、reward连接成的链。
return:一个trajectory中所有的reward的总和。通过比较return来评估策略是好是坏
Discounted rate : $\gamma \in [0,1)$ 。$discounted return = r_0 + \gamma r_1 + \gamma ^2 r_2 + …$ ,
$\gamma$ 通常表示是否更看重未来,$\gamma$ 越小,则越看重现在。
Episode: 能够到达terminal states(停止状态) 的trajectory。一个Episode也叫一个Episode task与之对应的是continuing task(指永无止境的任务)。
Markov decision process(MDP)
集合:
State:状态集合
Action:对于每个状态s的行动集合$A(s)$
Reward:奖励集合$R(s,a)$
概率要素(probability distribution):
State transition probability:$p(s’|s,a)$ 在状态s下,进行行动a,到达另一个状态$s’$的概率。
Reward probability: $p(r|s,a)$在状态s下,进行行动a,得到r的奖励的概率。
Policy: $\pi(a|s)$ 在状态s下,进行行动a的概率。
MDP的独特性质(markov property):与历史无关
$p(s{t+1} |a{t+1}st…a_1s_0) = p(s{t+1}|a_{t+1},s_t)$
$p(r{t+1} |a{t+1}st…a_1s_0) = p(r{t+1}|a_{t+1},s_t)$
第二章 贝尔曼公式
return
为什么return很重要?因为return评估的策略的好坏。
如何计算return?用$v_i$ 表示从$s_i$ 出发得到的return。
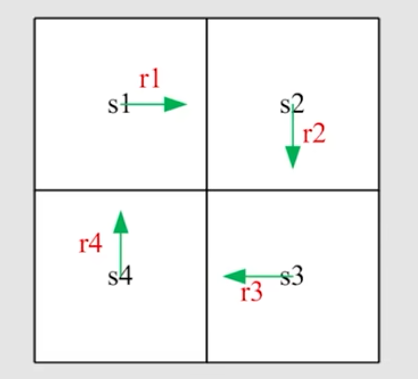
以下面的状态图为例:
那么根据定义有
$v_1 = r_1 + \gamma r_2 + \gamma^2 r_3 + …$
$v_2 = r_2 + \gamma r_3 + \gamma^2 r_4 + …$
$v_3 = r_3 + \gamma r_4 + \gamma^2 r_1 + …$
$v_4 = r_4 + \gamma r_1 + \gamma^2 r_2 + …$
也可以递推得到(Booststrapping):一个状态依赖于其他状态
$v_1 = r_1 + \gamma(r_2 + \gamma r_3 + …) = r_1 + \gamma v_2$
$v_2 = r_2 + \gamma(r_3 + \gamma r_4 + …) = r_2 + \gamma v_3$
$v_3 = r_3 + \gamma(r_4 + \gamma r_1 + …) = r_3 + \gamma v_4$
$v_4 = r_4 + \gamma(r_1 + \gamma r_2 + …) = r_4 + \gamma v_1$
然后就有$v = r + \gamma P*v$ ,这里的$v,r$ 是向量,$P$是变换矩阵。于是就能求解得出v的值。
state value
$St \overset{A_t}{\to} R{t+1},S{t+1}$ ,指在$S_t$ 下经过$A_t$ 得到$(R{t+1},S_{t+1})$
state value: $v_\pi(s) = \mathbb{E}[G_t|S_t=s]$当前状态为s的时候所有的return的期望值。
考虑下面的trajectory:$St \overset{A_t}{\to} R{t+1},S{t+1}\overset{A{t+1}}{\to} R{t+2},S{t+2}\overset{A{t+2}}{\to} R{t+3},S_{t+3}…$
那么$Gt = R{t+1} + \gamma R{t+2} + \gamma^2 R{t+3} + … = R{t+1} + \gamma G{t+1}$
则有
$v\pi(s) = \mathbb{E}[G_t|S_t=s] \ = \mathbb{E}[R_t|S_t = s] + \mathbb{E}[G{t+1}|S_t = s]$
公式中的第一项
$\mathbb{E}[R_{t+1}|S_t = s] = \underset{a}{\sum} [\pi(a|s) \underset{r}{\sum}p(r|s,a)r]$
公式中的第二项
- 于是,贝尔曼公式:
- 之后我们列出每个$si$对应的$v\pi(s_i)$的公式,然后求解方程组即可得到每个状态的state value。
贝尔曼公式的矩阵/向量形式
由贝尔曼公式:$v\pi(s)=\underset{a}{\sum} \pi(a|s) [\underset{r}{\sum}p(r|s,a)r+\gamma\underset{s’}{\sum}p(s’|s,a)v\pi(s’)]$
可以简略写为$v\pi(s) = r\pi(s) + \gamma \underset{s’}{\sum}p\pi(s’|s)v\pi(s’)$ , (这里有$r\pi(s) \iff \underset{a}{\sum} \pi(a|s)\underset{r}{\sum}p(r|s,a)r \ p\pi(s’|s) \iff \underset{a}{\sum} \pi(a|s)p(s’|s,a)$ )
对s进行标号得出$v\pi(s_i) = r\pi(si) + \gamma \underset{s_j}{\sum}p\pi(sj|s_i)v\pi(s_j)$
于是化为矩阵向量形式:$v\pi = r\pi + \gamma P\pi v\pi$ ,这里的$v\pi,r\pi$ 均为向量,$P\pi$ 为状态转移矩阵($[P\pi]{i,j} = p\pi(s_j | s_i)$ )
求解贝尔曼公式,进而得到state value是评判策略好坏(policy evaluation)的关键。
求解贝尔曼公式:
$v\pi = (I - \gamma P\pi)^{-1}r_{\pi}$ ,很简洁的公式,但是求逆太难算了。
迭代求法:$v{k+1} = r\pi + \gamma P_\pi v_k$
当$k \to \infty$时 ,有$vk = v\pi$
action value
从一个状态出发, 选择了一个action之后, 得到的return的期望。
在做判断时,根据Action value的大小来判断选择哪个Action。
求解状态s下进行行动a的action value($q_{\pi}(s,a)$)
计算action value:
- 根据state value求出
- 直接计算action value
第三章 贝尔曼最优公式
- 直观上地说,选择action value比较大的action,将他设置为1,其他设置为0。不断如此迭代,就可以找到最优的策略。
- 严格证明则需要贝尔曼最优公式。
如果对于所有的s,都有$v{\pi_1}(s) \ge v{\pi_2}(s) for\ all \ s \in S$ ,那么说$\pi_1$ 是比$\pi_2$要好的。
- 问题一:这样最优的策略是否存在?
- 问题二:这个最优的策略是唯一的吗?
- 问题三:策略是stochastic还是deterministic?
- 问题四:如何找到这么一个策略?
贝尔曼最优公式
- 贝尔曼最优公式堂堂登场!
可以发现,假设当$a = a’$时,$q(s,a)$ 最大,那么令$\pi(a|s) = \begin{equation} \left{ \begin{array}{lr} 1 &a = a’ \ 0 & a\not= a’ \end{array} \right. \end{equation} $ ,就会得到最大的$v(s)$。
即$v(s) = max(\underset{a}{\sum} (\pi(a|s) q(s,a)))=\underset{a\in A(s)}{max}(q(s,a))$
- 将公式变为矩阵-向量形式
我们设一个映射$f(v) := \underset{\pi}{max}(r\pi + \gamma P\pi v)$ ,那么原式就可以化为$v=f(v)$
一些概念
FixedPoint 不动点: 对于映射$f : X \to X$ ,存在$x \in X, f(x) = x$ ,那么x是不动点。
Contraction mapping : 在映射后两点的距离更小。$||f(x_1)-f(x_2)|| = \gamma||x_1 - x_2|| ,\gamma < 1$ 。(例如$f(x) = 0.5x$ 就是一个contraction mapping)
contraction Theorem
如果$f$是一个contraction mapping。那么一定有
- 存在一个$x$ , 满足$f(x^) = x^$ ,即$x^$ 是一个FixedPoint
- 这样的$x^*$ 一定有且只有一个
- 可以通过迭代算法求出这个$x^$ : $x_{k+1} = f(x_k)$ ,当$k \to \infty$ 时,有$x_k \to x^$
例如$f(x) = 0.5x$ ,那么$f(0) = 0, x^* = 0$ ,给出任意x,在不断进行$x = 0.5x$ 迭代后,会收敛于$0$
求解贝尔曼最优公式
可以证明在贝尔曼最优公式中$f(v) = \underset{\pi}{max}(r\pi + \gamma P\pi v)$ 是一个contraction mapping,那么$v = f(v)$ 。于是就可以通过迭代算法来求解出来。
假设$v^$ 是贝尔曼最优公式的解,即是他的不动点。即$v^ = \underset{\pi}{max}(r\pi + \gamma P\pi v^*)$
所以就可以利用contraction Theorem中的迭代算法来求得$v^*$
所以贝尔曼最优公式就是特殊的贝尔曼公式。
第四章 Value iteration & Policy iteration
Value iteration algorithm(值迭代算法)
值迭代算法就是根据贝尔曼最优公式来迭代求解优化问题。
$v{k+1} = f(v_k) = \underset{\pi}{max}(r\pi + \gamma P\pi v\pi)$
求解步骤:最开始生成一个任意的状态$v_0$ ,不断循环以下两步
- policy update更新策略:$\pi{k+1} = \underset{\pi}{argmax}(r\pi + \gamma P_\pi v_k)$
- value update 更新值: $v{k+1} = r{\pi{k+1}}+\gamma P{\pi_{k+1}} v_k$
需要注意的是$v_k$ 只是一个值,并不是一个state value。
不断迭代直到$vk-v{k-1}$ 足够小就认为已经收敛了。
Policy iteration algorithm(策略迭代算法)
最开始生成一个任意策略$\pi_0$
- policy evalution(PE): $v{\pi_k} = r{\pik} + \gamma P{\pik} v{\pi_k}$
- policy improvement(PI): $\pi{k+1}=\underset{\pi}{argmax}(r\pi + \gamma P\pi v{\pi_k})$
整体过程即$\pi0 \overset{PE}{\to}v{\pi0} \overset{PI}{\to}\pi_1\overset{PE}{\to}v{\pi1} \overset{PI}{\to}\pi_2\overset{PE}{\to}v{\pi_2} \overset{PI}{\to}\pi_3….$
几个核心问题:
在policy evaluation中如何求解 state value?
为什么进行PI后, $\pi_{k+1}$比$\pi_k$ 更优?
为什么最终能找到最优解?
Policy iteration和Value iteration 有什么关系?
Q1: 有两种方法(即求解贝尔曼公式的两种方法):
- closed-form solution : $v{\pi_k} = (I-\gamma P{\pik})^{-1} r{\pi_k}$
iterative solution: $v^{j+1}{\pi_k} = r{\pik} + \gamma P{\pik}v{\pi_k}^{(j)} , j = 0,1,2,…$
Q2: $\pi{k+1}=\underset{\pi}{argmax}(r\pi + \gamma P\pi v{\pik})$ ,因为$\pi{k+1}$ 一定比$\pi_k$ 要更大
Q3:$v{\pi_0} \le v{\pi1} \le v{\pi2} \le …\le v{\pi_k} \le v^*$
Q4: 二者是两个极端
truncated policy iteration algorithm
他是值迭代算法和策略迭代算法的推广,值迭代算法和策略迭代算法是truncated policy iteration algorithm的极端情况。
Policy iteration: $\pi0 \overset{PE}{\to}v{\pi0} \overset{PI}{\to}\pi_1\overset{PE}{\to}v{\pi1} \overset{PI}{\to}\pi_2\overset{PE}{\to}v{\pi_2} \overset{PI}{\to}\pi_3….$
Value iteration: $u_0\overset{PU}{\to}\pi_1’\overset{VU}{\to}u_1\overset{PU}{\to}\pi_2’\overset{VU}{\to}u_2…$
| Policy Iteration algorithm | Value iteration algorithm | Comments | |
|---|---|---|---|
| 1)Policy: | $\pi _0$ | N/A | |
| 2) Value: | $v{\pi_0} = r{\pi0}+\gamma P{\pi0} v{\pi_0}$ | $v0 := v{\pi_0}$ | |
| 3) Policy: | $\pi1 = \underset{\pi}{argmax}(r\pi + \gamma P\pi v{\pi_0})$ | $\pi1 = \underset{\pi}{argmax}(r\pi + \gamma P_\pi v_0)$ | 两个算法的第一步Policy是相同的。 |
| 4) Value: | $v{\pi_1} = r{\pi1} + \gamma P{\pi1} \textcolor{ #FF0000}{v{\pi_1}}$ | $v1 = r{\pi1} + \gamma P{\pi_1}\textcolor{ #FF0000}{v_0}$ | 两个算法求$v_\pi$ 的方法是不一样的 |
| 5)Policy: | $\pi2 = \underset{\pi}{argmax}(r\pi + \gamma P\pi v{\pi_1})$ | $\pi2’ = \underset{\pi}{argmax}(r\pi + \gamma P_\pi v_1)$ | |
| … | … | … | … |
区别在于计算$v_{\pi_1}$的时候是使用贝尔曼公式求,还是直接继承上一步的求法。
考虑公式$v{\pi_1} = r{\pi1} + \gamma P{\pi1} v {\pi_1}$
可以发现,value iteration就是在得到第一个$v$ 后就进行下一步操作;policy iteration则是不断你迭代直到收敛。 那么 truncated policy iteraion则是二者的结合,选择在中间的某一步停下。
第五章 MonteCarlo learning
蒙特卡洛方法是一个model-free RL的方法。(前面讲的算法都是model-based RL方法)
抛硬币例子
假设抛硬币问题: 抛一个硬币,正面价值为1,反面为-1,期望是多少?
那么 model-based方法:直接计算数学期望$\mathbb{E}[X] = \underset{x}{\sum}xp(x) = 10.5+(-1)0.5 = 0$
结果很精确,但是通常很难找到这样的数学模型。
model-free方法:做实验,随机扔硬币,然后统计值,最终可以得到近似值。
一个简单的MC-based RL算法
(我们称这个算法为MC-basic算法)
可以通过改变Policy iteration算法来变成model-free 算法。
- policy evalution(PE): $v{\pi_k} = r{\pik} + \gamma P{\pik} v{\pi_k}$
- policy improvement(PI): $\pi{k+1}=\underset{\pi}{argmax}(r\pi + \gamma P\pi v{\pi_k})$
$\pi{k+1}(s) = \underset{\pi}{argmax} \underset{a}{\sum}\pi(a|s)\textcolor{ #FF0000}{q{\pi_k}(s,a)}$
关键在于计算$q_{\pi_k}(s,a)$ , 两种方法:
- 需要模型:$q{\pi_k}(s,a) = \underset{r}{\sum}p(r|s,a)r + \gamma \underset{s’}{\sum}p(s’|s,a)v{\pi_k}(s’)$
- 不需要模型:$q_{\pi_k}(s,a) = \mathbb{E}[G_t|S_t=s,A_t=a]$
基于蒙特卡洛的model即通过大量采样来估计$G_t$
MC exploring Starts
遵循策略$\pi$ ,我们会得到一个episode如下:
$s_1 \overset{a_2}\to s_2\overset{a_4}\to s_1\overset{a_2}\to s_2\overset{a_3}\to s_5\overset{a_1}{\to}…$
定义Visit;一个episode中访问的$(state,action)$对的数量。
在MC-basic方法中,使用的是Initial-visit method,即只考虑$s_1 \overset{a_2}{\to}$ 这一个(state,action)对。这导致了没有充分利用了整个episode。
那么对于一个episode:
因此我们就可以通过这一个episode来估计$(s_1,a_2),(s_2,a_4),(s_1,a_2),(s_2,a_3),(s_5,a_1),\dots$ 的action value。而不是仅仅用于$(s_1,a_2)$ 。
- first-visist : 指在遇到相同的(state,action)时,只使用第一次遇到的。
- every-visit:指在遇到相同的(state,action)时,每个都做考虑,最后综合起来。
generalized policy iteration(广义策略迭代):指并不是精确求解的代码,使用迭代来得到策略,像truncated policy iteration algorithm和 MC都属于generalized policy iteration 。
soft policies
因为我们从一个(state,action)出发能够到达多个状态,所以我们也就没必要把所有的(state,action)都设置为出发点了。
那么如何选择出发点?
$\epsilon-greedy\ policies$ : $\pi(a|s)= \begin{equation} \left{ \begin{array}{lr} 1-\frac{\epsilon}{|A(s)|}(|A(s)|-1) &for\ the\ greedy\ action \ \frac{\epsilon}{|A(s)|} & for\ the\ other\ |A(s)|-1\ actions \end{array} \right. \end{equation}$
这里的greedy action指的就是$q_\pi(s,a^*)$ 最大的那个action。($\epsilon$通常很小), 这样在保证greedy action被选择的概率较大的情况下,其他的action同样有一些概率被选择。
- $\epsilon-greedy\ policies$能够平衡$exploitation$和$exploration$
exploitation:指的是充分利用value,贪心于当前。
exploration:指的是探索当前非最佳的情况,可能会找到未来更优的情况。
这样选择一个(state,action)作为出发点,就可以通过exploration来得到所有的(state,action)的策略。
MC $\epsilon$-Greedy algorithm
对于之前的方法,只会选择最优的action,即$a^*$ 。
$\pi{k+1}(s) = arg\ \underset{\textcolor{ #0000FF}{\pi \in \Pi{\epsilon}}}{max}\underset{a}{\sum}\pi(a|s)q_{\pi_k}(s,a)$
那么对于MC $\epsilon$-Greedy algorithm
便是给了其他action一个较小的$\frac{\epsilon}{|A(s)|}$
$\epsilon$-Greedy algorithm 中的$\epsilon$ 较大的时候,探索性很强,但是最优性比较差。
我们可以通过起初设置较大的$\epsilon$,然后逐渐减小他来平衡探索性和最优性。
第六章 Stochastic Approximation & Stochastic Grandient Descent
Stochastic Approximation(随机近似理论) 和Stochastic Grandient Descent(随机梯度下降)
Motivating example
mean estimation problem:
- 考虑有一个随机变量 X
- 目标是计算期望 $\mathbb{E}[X]$
- 假设我们有N个采样${xi}{i=1}^N$
- 那么期望可以被估计为$\mathbb{E}[X] \approx \overline{x}:=\frac{1}{N}\underset{i=1}{\overset{N}{\sum}}x_i$
- 当$N \to \infty$ ,$\overline{x} \to \mathbb{E}[X]$
怎么计算$mean\ \overline{x}$ ?
方法一: 计算所有的总和,然后除以$N$
方法二(iterative mean estimation):实时估计$\overline{x}$ ,当出现新的$x_i$时,更新$\overline{x}$
我们规定$w{k+1}$ 表示前$\textcolor{ #0000EE}{k}$个x的均值。即$w{k+1} = \frac{1}{k}\underset{i=1}{\overset{k}{\sum}}x_i $ 。(一般设置$w_1 = x_1$)
那么根据如下公式
我们就可以迭代地计算$w_{k+1}$ 了。
于是我们稍作改进,把$\frac{1}{k}$ 换成$\alpha$ .于是我们就可以通过调整$\alpha$ 来改变公式的计算了。
Robbins-Monro algorithm
stochastic approximation能够做到在不知道函数具体公式的情况下求出解。
RM算法是stochastic approximation中的开创性工作。
而stochastic gradient descent algorithm 则是RM的一种特殊情况。
问题:求解$g(w) = 0$方程, 其中$w$是未知量,$g$是函数。
于是RM算法可以求解如下问题:
$w_{k+1} = w_k - a_k \tilde g(w_k,\eta _k)$
其中$\eta _k$ 是噪声, $\tilde g(w_k,\eta _k) = g(w_k) + \eta_k$ ,$\alpha$是一个正数 。
函数$g(w_k)$ 是一个黑盒函数,我们无法得出它的具体公式。
不断迭代这个公式,就能够收敛到$g(w) = 0$
RM算法-Convergence properties
RM算法的三个条件:
$0 < c_1 \le \nabla _wg(w) \le c_2$ ,即导数大于0,并且不会趋于无穷。
$\sum{k=1}^{\infty}a_k = \infty$ 并且$\sum{k=1}^{\infty}a_k^2 < \infty$ 。
$\sum_{k=1}^{\infty}a_k^2 < \infty$ 保证了$a_k$一定会收敛到0。
$\sum_{k=1}^{\infty}a_k = \infty$ 保证了$a_k$收敛的不会太快,否则加起来就不会是无穷了。
$\mathbb{E}[\eta_k] = 0$ 并且$\mathbb{E}[n_k^2|\mathcal{H}]<\infty$ (这里的$\mathbb{E}[\eta_k^2|\mathcal{H}]$的意思是$\eta_k$的方差)。通常这里的噪声通过同分布(Independent and Identically Distriuted)采样得来,并且在此处$\eta_k$并没有强制要求满足高斯分布。
对于条件二的解释:
根据上面的公式$w{k+1}-w_k = a_k \tilde g(w_k,\eta_k)$ ,那么$a_k$收敛到0,才能保证$w{k+1}-w_k$不断收敛到0,从而趋于稳定。
而将$k = 1,2,…,\infty$ 的公式相加可以得到
$w_{\infty} - w_1 = \overset{\infty}{\underset{k=1}{\sum}}a_k \tilde g(w_k,\eta_k)$ .
$w^ \approx w\infty$是我们猜测的值,$w_1$ 是初始值,那么$\sum{k=1}^{\infty}a_k = \infty$ 保证了不管我们选的初始值$w_1$离目标值有多远,最终都可以通过不断迭代得到$w^$
$a_k$取什么值是符合条件的? $a_k= \frac{1}{k}$ 。(但一般在$k$很大的时候,不会让$a_k$一直变小,达到某个较小值后则会不再改变)
SGD(stochatic gradient descent)
目标是解决如下优化问题:
$\underset{w}{min} J(w) =\mathbb E[f(w,X)]$
算法一、 gradient descent(GD)梯度下降法:
$w_{k+1} = w_k- \alpha_k \nabla_w \mathbb E[f(w_k,X)] = \alpha_k\mathbb E[\nabla_wf(w_k,X)]$
这里的$\alpha_k$ 是步长,就是学习率。 但是一般无法得到准确的梯度的期望。
算法二、batch gradient descent(BGD)批量梯度下降法:
$\mathbb [\nabla_w f(w_k,X)] \approx \frac{1}{n} \underset{i=1}{\overset{n}{\sum}}\nabla_wf(w_k,x_i)$
于是得到:$w_{k+1} = w_k- \alpha_k\frac{1}{n} \underset{i=1}{\overset{n}{\sum}}\nabla_wf(w_k,x_i)$
不需要求期望,用多次采样的平均值来代替期望值,但是每次都需要求n个数的平均太耗时了。(n为采样次数)
算法三、stochastic gradient descent(SGD) 随机梯度下降:
$w_{k+1} = w_k - \alpha_k \nabla_w f(w_k,x_k)$
和GD相比,替使用随机梯度来替换准确的期望的梯度。
和BGD相比,其实就是把n设置为了1。
SGD 的例子和练习
假设如下例子:$\underset{w}{min} \ J(w) = \mathbb E[f(w,X)] = \mathbb E[\frac{1}{2} ||w-X||^2]$
此处的$f(w,X)= ||w-X||^2/2, \nabla_wf(w,X) = w - X$
三个练习:
- 证明最优解$w^$ 满足$w^ = \mathbb E [X]$
- 这个例子的GD算法是什么?
- 这个例子的SGD算法是什么?
不求期望了,直接用某一个的$w_k - x_k$ 来代替$\mathbb E[w_k - X]$
我们发现最后的公式和mean alogrithm算法是一样的,所以mean algorithm算法就是一种特殊的SGD算法。
SGD算法的收敛性(convergence)
- 首先证明SGD是一种特殊的RM算法:
SGD的目标是最小化$J(w) = \mathbb E[f(w,X)]$ , 这个问题可以转换为寻根问题:
$\nabla_w \ J(w) = \mathbb E[\nabla _w f(w,X)] = 0$
设$g(w) = \nabla_w J(w) = \mathbb E[\nabla_wf(w,X)]$
那么SGD的目标就是找到$g(w)= 0$的根。
我们可以测量的是:
而与之对应的RM算法是
- 接下来我们就可以应用RM算法的收敛性条件,来证明SGD是收敛的。
SGD算法的收敛模式
SGD收敛的过程中,是否会收敛很慢或者收敛随机?
我们定义相对误差$\delta _k$
此处的$\mathbb E[\nabla_w f(w,X)]$是true gradient, 而$\nabla_wf(w,x)$ 是 stochastic gradient。
性质:当$w_k$ 离$w^$ 较远时,相对误差较小, 当$w_k$ 离$w^$ 很近的时候,才会有比较大的相对误差(即随机性)
如何得到如上性质?
使用拉格朗日中值定理$f(x_1)-f(x_2) =f’(x_3)(x_1 - x_2)$
那么由$\mathbb E[\nabla _wf(w^*,X)] = 0$和中值定理 ,我们有
我们假设$\nabla^2_wf \ge c > 0$
那么我们考虑分母项,就有
于是误差$\delta_k$满足
于是当$w_k$ 距离$w^*$比较远,那么分母比较大,相对误差$\delta_k$ 的上界比较小。
当$w_k$ 距离$w^*$比较近,那么分母比较小,此时相对误差$\delta_k$ 的上界才会变大一些。
BGD,MBGD和SGD
- BGD(batch gradient descent) , 用到所有的采样来平均求期望
- MBGD(min-batch gradient descent) ,选择一部分采样(m个采样)
- SGD(stocastic gradient descent) ,选择一个采样
在MBGD中,当MBGD中的采样数量$m=1$时,等价于SGD。
当采样数量$m = n$时,趋近于BGD(注意!此时不完全等于BGD,因为BGD是取出所有的n个样本,而MBGD是对样本集进行n次的采样)
考虑如下优化问题:
$\underset{w}{min} \ J(w) = \frac{1}{2n} \underset{i=1}{\overset{n}{\sum}} ||w - x_i || ^2$
那么三种算法的迭代公式如下:
第七章 Temporal-Difference learning
Temporal-Difference learning (TD)时序差分算法
这是一个incremental 迭代式的算法。
motivating example
- 先考虑一个简单的问题 mean estimation : 计算
$w = \mathbb[X]$ , (X是一些iid(独立同分布)采样${x}$)
令$g(w) = w - \mathbb E[X]$ ,则有
$\tilde g(w,\eta) = w - x = (w - \mathbb E[X]) + (\mathbb E[X] - x) \approx g(w) + \eta$
然后根据RM算法,可以得到$w_{k+1} = w_k - \alpha_k \tilde g(w_k,\eta_k) = w_k - \alpha _k (w_k - x_k)$
- 考虑一个复杂一些的例子:计算
$w = \mathbb E[v(X)]$ , (X是一些iid(独立同分布)采样${x}$)
令$g(w) = w - \mathbb E[v(X)]$
$\tilde g(w,\eta) = w - v(x) = (w - \mathbb E[X]) + (\mathbb E[X] - v(x)) \approx g(w) + \eta$
然后根据RM算法,可以得到$w_{k+1} = w_k - \alpha_k \tilde g(w_k,\eta_k) = w_k - \alpha _k (w_k - v(x_k))$
- 第三个例子:计算
$w = \mathbb [R + \gamma v(X)]$ , ($R,X$ 是随机变量,$\gamma$ 是常量,$v(\cdot)$ 是函数)
令$g(w) = w - \mathbb E[R + \gamma v(X)]$ ,
然后根据RM算法,可以得到$\textcolor{ #0000FF}{w_{k+1} = w_k - \alpha_k \tilde g (w_k,\eta_k) = w_k - \alpha_k[w_k -(r_k + \gamma v(x_k))]}$
TD算法中的state values
注意:
- TD算法通常指的是一大类的RL算法。
- TD算法也可以特指一种用于估计state values的算法。
TD算法基于数据:$(s0,r_1,s_1,…,s_t,r{t+1},s{t+1},…)$ 或者${(s_t,r{t+1},s_{t+1})}_t$ ,这种数据通过给定的策略$\pi$ 来生成。
TD算法则是:
对于公式$(2)$ 表示,如果现在的状态是$s_t$ ,那么其他状态的value是不更新的。
我们关注于第一个式子:
$v{t+1}(s_t) = v_t(s_t) - \alpha_t(s_t)[v_t(s_t) - [r{t+1} + \gamma vt(s{t+1})]]$
其中的$v_{t+1}(s_t)$ 是新的估计值,$v_t(s_t)$ 是现在的估计值。
$vt(s_t) - [r{t+1} + \gamma vt(s{t+1})]$ 是误差$\delta_t$
$[r{t+1} + \gamma v_t(s{t+1})]$ 是目标$\overline v_t$
为什么$\overline v_t$ 是“TD目标” ?因为每次$v(s_t)$ 都会向着 $\overline v_t$ 移动。
因为$0 < 1 - \alpha_t(s_t) < 1$
于是$|v{t+1}(s_t) - \overline{v}_t| \le |v{t}(s_t) - \overline{v}_t|$
为什么 $\delta_t$是“TD error”?
$\deltat = v(s_t) - [r{t+1} + \gamma v(s_{t+1})]$
因为发生在t和t+1两个时刻 ,所以才叫时序差分,
TD error 描述了$vt$ 和$v\pi$ 之间的误差。
当$vt = v\pi$ 时,那么应该有$\delta _t = 0$ 。
TD error是一种 innovation,这是经验$(st,r{t+1},s_{t+1})$的一种新的信息。
TD算法的数学意义
他解决了给定$\pi$,求解贝尔曼公式。
新的贝尔曼公式:
在这之中G是下个状态的Reward,所以$\mathbb E[G|S = s] $可以表示为:
其中$S’$ 是下一个状态
于是s的state value可以写为:
这个公式也被称为贝尔曼期望公式。
接下来使用RM算法来求解这个贝尔曼期望公式:
定义$g(v(s)) = v(s) - \mathbb E[R + \gamma v_\pi(S’)| S = s] = 0$
于是我们有$g(v(s)) = 0$
在这之中,$g(v(s)) = (v(s) - \mathbb E[R + \gamma v\pi(S’)| s]) $ ,误差$\eta = E[R + \gamma v_pi(S’)| s] - [r + \gamma v\pi (s’)]) $
那么与之对应的RM算法是:
这里的$vk(s)$代表$v\pi(s)$在第k步的估计,而$r_k,s’_k$ 是第k步中从$R,S’$中取出的样本。
对公式做以下替换:
将一组采样${(s,r,s’)}$ 替换为一组序列${st,r{t+1},s_{t+1}}$, 从而做到对所有的s都进行更新。
将$v\pi(s’)$ 换为$v_k(s’_k)$ ,即我们直接用$s’$ 在第k步的估计值来替代真实值。 虽然会有一些偏差,但是最终会收敛到$v\pi$
TD算法的收敛:
对于所有状态$s \in S$ 。当$t \to \infty$ 时, $vt(s)$ 以概率1收敛到策略$\pi$ 下的状态值函数$v\pi(s)$。
如果对于所有的状态$s \in S$ ,步长参数序列$\alpha_t(s)$ 都满足$\sum_t\alpha_t = \infty$ 并且$\sum_t\alpha_t^2(s) < \infty$ 那么上述收敛成立。
| TD/Sarsa learning | MC learning |
|---|---|
| online:TD学习是在线的,在接收到一个奖励后可以更新state/action value | Not online:MClearning是非在线的,必须等到整个episode已经完成之后,计算return值然后进行估计。 |
| continuing tasks:即能处理一直持续下去的任务,同时也能解决episodic tasks。 | Episodic tasks:必须是有限步的episode,才能等到他的返回值。 |
| Bootstrapping:会基于之前对状态的猜测,加上一些新的信息来形成一个新的猜测 | Non-boostrapping:直接根据当前的episode计算return,不涉及到之前的估计值 |
| Low estimation variance :在算法过程中涉及到的随机变量比较少,所以方差会比较小 | High estimation variance:它涉及到了很多的variable,因为一次episode会涉及到很多的Reward,而只用其中一次的采样,所以就会有比较大的方差。 |
| bias:因为基于之前的经验,所以可能会因为之前的经验而产生bias,导致有偏估计,但是在不断增加经验后还是会趋于正确结果 | no bias:不基于之前的估计,所以不会产生bias |
TD算法中的action values:Sarsa
Sarsa是经验集$(st,a_t,r{t+1},s{t+1},a{t+1})$ 的拼接。
TD算法是用来估计给定策略$\pi$ 的state value,但我们需要估计的是action value。下面引入Sarsa。
假设我们有如下经验${(st,a_t,r{t+1},s{t+1},a{t+1}) }_t$ ,那么我们定义Sarsa公式如下:
这个式子和TD算法几乎一样,只是类似地把$v_t(s_t)$ 改成了$q_t(s_t,a_t)$这样子。
Sarsa的数学意义和TD也是几乎一样的。(如贝尔曼公式,收敛性等)
Sarsa所求解的贝尔曼公式:
收集经验:$(st,a_t,r{t+1},s{t+1},a{t+1})$ ,遵循$\pit(s_t)$执行$a_t$ ,得到$r{t+1}$的奖励,然后走到状态$s{t+1}$ 并遵循$\pi{t}(s{t+1})$ 来采取行动$a{t+1}$ 。
更新q值(q value update/policy evaluaton):$q{t+1}(s_t,a_t) = q_t(s_t,a_t) - \alpha_t(s_t,a_t)[q_t(s_t,a_t) - [r{t+1} + \gamma qt(s{t+1},a_{t+1})]]$
更新策略policy(policy update/policy improvement):
注意这里的PE和PI是立刻执行的,而不是等return之后再精确计算。
注意这个策略是一个$\epsilon- greedy$策略,也就是说倾向于采取qvalue最大的action,但是其他的action同样有概率取到。
Expected Sarsa
公式如下:
此处的$\mathbb E[qt(s{t+1},A)] = \underset{\pi}{\sum}\pit(a| s{t+1})qt(s{t+1},a) \approx vt(s{t+1})$
和普通的sarsa的区别是用$(r{i+1} + \gamma \mathbb E [q_t(s{t+1},A)])$ 替换了$r{t+1}+\gamma q_t(s{t+1},a_{t+1})$.
不再需要$a_{t+1}$ 了,随机性会减小一些,但是需要更大的计算量。
Expected Sarsa的数学意义也是在求解贝尔曼公式:
$q\pi(s,a) = \mathbb E[R{t+1} + \gamma \mathbb E{A{t+1} \sim \pi(S{t+1})}[q\pi(S{t+1},A{t+1})]|S_t = s,A_t = a]$
n-step Sarsa
是Sarsa的一个推广,包含了Sarsa和蒙德卡罗方法。
我们的action value如下定义:$q_\pi(s,a) = \mathbb E[G_t|S_t=a,A_t=a]$
那么$G_t$ 可以被写成如下形式:
所以n-step Sarsa对应的贝尔曼公式是:
n-step Sarsa需要的数据是$(st,a_t,r{t+1},s{t+1},a{t+1},…,r{t+n},s{t+n},a_{t+n})$
所以他的数据需要等到$t+n$ 时刻,才能进行更新。是online和offline的结合。
- 当n比较大的时候,更接近于MC,会有比较大的variance,比较小的bias。
- 当n比较小的时候,更接近于Sarsa,会有比较小的variance,比较大的bias。
TD中最优action value学习:Q-learning
算法如下:
和Sarsa相比,用$r{t+1} + \gamma \underset{\alpha \in \mathcal A}{max}\ q_t(s{t+1},a)$ 替换了$r{t+1} + \gamma q_t(s{t+1},a_{t+1})$
Q-learning求解的数学问题是(不是在求解贝尔曼方程):
求解一个贝尔曼最优方程:
off-policy 和 on-policy
两种策略:
- behavior policy用来生成经验样本
- target policy不断地更新来将target policy更新到optimal policy。
基于这两种策略,可以分为两类算法:
- on-policy: 其中的behavior policy和target policy是相同的,即用自己的策略来和环境交互,然后得到经验并改进自己的策略,之后再用相同的策略和环境交互。
- off-policy:用一个策略和环境交互得到大量经验,然后用这些经验来不断改进策略(一步到位,不再通过新的策略引入新的经验)
on-policy的好处就是可以不断接收新的经验,实时更新策略。
off-policy的好处就是可以直接使用别人已经获取过的经验。如用之前通过探索性较强的算法得到的经验。
如何判断一个TD算法是on-policy还是off-policy?
- 看这个TD算法是在解决什么样的数学问题
- 看在算法的执行过程中需要什么东西才能使算法跑起来
- Sarsa是on-policy的:
Sarsa在数学上就是在求解一个贝尔曼公式:
此处的$R \sim p(R|s,a),S’ \sim p(S’|s,a),\textcolor{0xFF0000}{A’ \sim \pi(A’|S’)}$
Sarsa在算法中:
如果给定了$(st,a_t)$ 那么$r{t+1}$和$s_{t+1}$和任何策略无关,和$p(r|s,a),p(s’|s,a)$有关。
$a{t+1}$是由策略$\pi_t(s{t+1})$ 产生。 所以$\Pi_t$ 既是behavior policy也是target policy
- MC learning 是on-policy的:
MC目的是求解如下贝尔曼方程:
MC的实现是
我们用策略$\Pi$ 来得到trajectory经验,然后得到return来近似估计$q_\pi$ 进而改进$\Pi$
- Q learning 是off-policy的:
Q learning求解的数学问题是:
求解贝尔曼最优公式:
Q learning的实现过程是:
需要的经验是$(st,a_t,r{t+1},s_{t+1})$
注意这里的经验不包含$a_{t+1}$
如果$(st,a_t)$ 给定,那么$r{t+1}$ 和$s_{t+1}$ 不依赖于策略。
behavior policy是从$s_t$ 出发得到$a_t$
target policy 是根据$q_\pi$ 来选择action
Q-learning 的实施
如果将Q-learning中的behavior policy 和target policy强行设置为一致的,那么它可以是on-policy的:
对每个episode执行以下三步
收集经验$(st,a_t,r{t+1},s{t+1})$ ,在这一步根据$\pi_t(s_t)$ 采取行动$a_t$ 来生成$(r{t+1},s_{t+1})$
更新q-value:$q{t+1}(s_t,a_t) = q_t(s_t,a_t) - \alpha_t(s_t,a_t)[q_t(s_t,a_t) - [r{t+1} + \gamma maxa \ q_t(s{t+1},a)]]$
更新policy:
也可以是off-policy的:
对每个episode生成策略$\pi_b$ (这里的b代表behavior),这个策略用来生成experience
对episode的每一步$t = 0,1,2,…$ 执行以下两步:
更新q-value:$q{t+1}(s_t,a_t) = q_t(s_t,a_t) - \alpha_t(s_t,a_t)[q_t(s_t,a_t) - [r{t+1} + \gamma maxa \ q_t(s{t+1},a)]]$
更新target policy:
注意这里的第三步是greedy不是$\epsilon-greedy$ ,因为我们不需要新的策略来生成经验,所以也就不需要使用$\epsilon-greedy$ 来增加探索性,只需要保证最优性。
使用off-policy的话,使用的behavior policy最好是探索度比较强的策略,否则可能得不到好的target policy。
TD的统一表示
所有的TD算法都能用如下公式表达:
这里的$\overline{q}_t$ 就是TD target。
TD算法的目标就是接近TD target ,减小TD error
| 算法 | $\overline q_t$ 的表示 | |
|---|---|---|
| Sarsa | $\overline qt = r{t+1} + \gamma qt(s{t+1},a_{t+1})$ | |
| n-step Sarsa | $\overline qt = r{t+1} + \gamma r{t+2} +… + \gamma ^ nq_t(s{t+n},a_{t+n})$ | |
| Expected Sarsa | $\overline qt = r{t+1} + \gamma \underset{a}{\sum}\pi_i(a | s{t+1})q_t(s{t+1},a)$ |
| Q-learning | $\overline qt = r{t+1} + \gamma \underset{a}{max}qt(s{t+1},a)$ | |
| Monte Carlo | $\overline qt = r{t+1} + \gamma r{t+2} + \gamma^2r{t+3} +…$ |
第八章 value function Approximation
在此之前,所有的state value和action value都是用表格表示出来的,例如:
| $a_1$ | $a_2$ | $a_3$ | $a_4$ | $a_5$ | |
|---|---|---|---|---|---|
| $s_1$ | $q_\pi(s_1,a_1)$ | $q_\pi(s_1,a_2)$ | $q_\pi(s_1,a_3)$ | $q_\pi(s_1,a_4)$ | $q_\pi(s_1,a_5)$ |
| … | … | … | … | … | … |
| $s_9$ | $q_\pi(s_9,a_1)$ | $q_\pi(s_9,a_2)$ | $q_\pi(s_9,a_3)$ | $q_\pi(s_9,a_4)$ | $q_\pi(s_9,a_5)$ |
使用表格的好处就是可以直观地分析
坏处就是无法处理很大的state space 或者action space、无法处理连续的state和action。泛化能力不强。
Value Function Approximation的含义
使用直线来拟合点:
$\hat v(s,w) = as + b = [s,1]\bigl[ \begin{smallmatrix}a \b \end{smallmatrix}\bigr] = \phi ^T(s)w$
这里的w是parameter vector(参数向量)
$\phi(s)$ 是s的feature vector(特征向量)
$\hat v (s,w)$ 是w的linear(线性关系)
使用函数来拟合可以节省存储空间(只需要存w的值(a,b)即可)
缺点是拟合后不太精确。
同样可以用二次函数来拟合:
$\hat v (s,w) = as^2 + bs + c = \phi^T(s)w$
(需要注意的是,这样的曲线对于w来说同样是一种线性的拟合)
- 使用Value Function Approximation的优点:
- 便于存储,只需要存储w即可,不用存储大量数据。
- 泛化能力更强,假设s2进行了更改,在表格存储中只会更改s2对应的内容,而使用value function approximation则会改变w的值,从而影响其他的值(如s1和s3),这样会增强泛化能力
objective funciton
令$v_\pi(s)$ 作为真正的state value。 $\hat v(s,w)$是函数的近似值。
我们目标就是找到最优的w来使得$\hat v(s,w)$ 可以很好的拟合出$v_\pi(s)$
目标函数objective function如下:
我们目标就是找到最好的w使得$J(w)$ 最小化。
求解期望常见的两种方法:
uniform distribution 平均分布:
认为每一个状态都是同等重要的。那么每一个状态的权重就是$\frac{1}{|S|}$
使用均匀策略的缺点是,我们将很远处的状态和距离目标近处的状态设置权重一样。导致没有侧重点
第二个概率分布:
stationary distribution:
这是一种Markov下的long-run behavior
让${d\pi(s)}{s\in S}$ 作为在策略$\pi$ 下的Markov stationary distribution,通过定义$d\pi(s) \ge 0 \text{ and } \underset{s \in S}{\sum}d\pi(s) = 1$
于是目标函数objective function可以被写为:
Stationary distribution 也被称为steady-state distribution 或者limit distribution。
怎么求$d_\pi(s)$ ?给出一个很长很长的episode:
我们定义$n\pi(s)$ 表示s出现的次数。于是我们用频率来近似估计$d\pi(s)$
我们没必要真正的模拟这个episode并统计次数,可以通过数学公式得到:
最终趋于稳定的$d_\pi^T$ 要满足:
这里的$P_\pi$ 是一个矩阵,代表从$s$ 到$s’$ 转移的概率$p(s’|s)$
optimization algorithms
目标函数的优化算法(optimization algorithms of objective function)
为了最小化目标函数$J(w)$ ,我们可以使用梯度优化gradient-descent
这里的true gradient是:
但是求期望很麻烦,所以我们用sotcastic gradient descent来替代gradient descent
但是在现实中,我们是无法得知$v_\pi(s_t)$ 的。
有如下方法:
Monte Carlo learning 和 value function approximation结合
让$g_t$ 表示从$s_t$ 开始的episode的return。那么
$w_{t+1} = w_t + \alpha_t(g_t-\hat v(s_t,w_t)) \nabla_w \hat v (s_t,w_t)$
TD learning 和value function approximation结合
在TD算法中可以用$r{t+1}+\gamma \hat v (s{t+1},wt)$ 来作为$v\pi(s_t)$ 的一个估计值。于是有
$w{t+1} = w_t + \alpha_t[r{t+1}+\gamma \hat v (s_{t+1},w_t) - \hat v(s_t,w_t)] \nabla_w \hat v(s_t,w_t)$
目前只能用来估计给定策略的state values。
selection of function approximators
函数的选取方法
选择线性函数(之前广为使用):
此处的$\phi(s)$ 是特征向量,他是基于多项式的(polynomial basis),基于傅里叶的(Fourier basis),…
选择神经网络(现在广为使用):
网络的参数是w,神经网络的输入是state,输出是估计值$\hat v (x,w)$
考虑线性函数:$\hat v (s,w) = \phi^T(s)w$ ,我们有
代入TD算法可以得到TD-Linear:
Linear function approximation的劣势:、
- 很难去选择一个合适的feature vectors
Linear function approximation的优势:
- 数学原理清晰,能够可以帮助我们更透彻地研究。
- 表征能力还算可以。表格形式tabular representation是Linear function approximation 的特殊形式。
Tabular representation 是Linear funciton的一种特殊情况:
首先考虑如下的特征向量:
这里的$e_s$ 是一个只有一个1,其他都是0的向量。
那么这样的话$\hat v(s,w) = e_s^T w = w(s)$ , 这样$w(s)$ 就是w的第s个元素了。也就是tabular representation。
然后我们把$\phi(s_t) = e_s$ 带入到TD-Linear中。
因为$e_{s_t}$ 只有在$w_t$ 的位置是1,其他位置是0,所以在$w_t$ 中只有$S_t$的位置被更新了。
于是我们发现这个式子和之前tabular的TD算法是一样的。
Sarsa
Sarsa和value function estimation结合:
除了标蓝的地方略有差别,其他和tabular是一样的。
- 因为我们描述的参数从state变为了parameter, 所以更新的内容从$q(s,a)$变为了$w$
- 使用估计值来估计一个点的state,所以原先的$q(s,a)$ 变为了由函数估计产生的$\hat q(s,a,w)$
- 最后乘上$\hat q$ 的梯度来使得向零点移动。
步骤如下:
对每个episode 执行如下操作:
遵循$\pit(s_t)$ 执行动作$a_t$ ,然后生成$r{t+1},s{t+1}$ ,然后遵循$\pi_t(s{t+1})$执行$a_{t+1}$ .
更新值(parameter update):
更新策略(policy update):
Q-learning
Q-learning 和value function estimation 结合:
蓝色部分为value function estimation 版本的Q-learning和tabular 版本之间的区别。
步骤如下(on-policy):
对每个episode 执行如下操作:
遵循$\pit(s_t)$ 执行动作$a_t$ ,然后生成$r{t+1},s_{t+1}$
更新值(parameter update):
更新策略(policy update):
Deep Q-learning(deep Q-network)
首先定义损失函数:objective function/loss function:
这是一个贝尔曼最优误差,下式为Q-learning的Bellman optimality error:
因此$R+ \gamma \underset{\alpha \in \mathcal A(S’)}{max} \hat q(S’,a,w) - \hat q(S,A,w)$ 的期望应该是0.
如何最小化这个损失函数? 使用梯度下降法 Grradient-descent:
求$J(w)$ 关于w的梯度,难点在于表达式中由两个地方出现了$w$ ,于是基本思想为我们把前半部分当作一个常数y:
这样就只有$\hat q(S,A,w)$ 项包含w了,就可以比较简单地求解梯度。
求解方法:
引入两个网络
- main network 表示$\hat q(s,a,w)$
- target network $\hat q(s,a,w_T)$
将损失函数改写为:
即我们保持target network一段时间不动,因此就能将前半部分作为常数,然后来更新main network。 之后再更新target network。这样也能保证两个网络最后都收敛。
DQN-Experience replay
Experience replay经验回放 ,具体为:
- 我们在收集完数据后,并不根据他们被收集的顺序来使用他们。
- 而是我们把他们存储到一个集合replay buffer 中, $\mathcal B = { (s,a,r,s’) }$
- 每次训练神经网络的时候, 把他们混到一起,然后取出一些样本(mini-batch)来进行训练。
- 在取出样本的时候一定要服从均匀分布(uniform distribution)
为什么需要经验回放?为什么必须服从均匀分布?
我们观察损失函数:
- $(S,A) \sim d$ 我们根据索引(S,A) 就能够找到一个唯一的随机变量d
- $R \sim p(R|S,A) ,S’ \sim p(S’|S,A)$ , R和S’ 由给定的模型决定。
- 在数据采集的时候,我们可能并不是按照均匀分布采样的。因为他们被确定的策略产生。
- 为了打破连续样本之间的相关性(通常他们有很强的时间相关性),我们可以从replay buffer中进行随机均匀采样。
- 这就是为什么经验回放是必须的,并且是必须均匀分布采样的。
Deep Q-learning
off-policy version:
目标是从通过 behavior policy $\pi_b$ 生成的一些经验中学习一个优化的target network来逼近最优action values 。
步骤如下:
- 存储由behavior policy 生成的经验,存放到replay buffer中 $\mathcal B = {(s,a,r,s’)}$
- 对每一次迭代重复如下动作:
- 从$\mathcal B$ 中均匀提取一些样本(mini-batch)
- 对于每个样本$(s,a,r,s’)$ ,计算target value $yT = r+ \gamma\ max{\alpha \in \mathcal A(s’)}(\hat q ,a,w_T)$ , 在这之中$w_T$ 是target network(两个网络之一)
- 使用mini-batch${(s,a,y_T)}$ 更新main network 来最小化$(y_T - \hat q (s,a,w))^2$
- 每进行C次迭代,更新target network:$w_T = w$
第九章 Policy Function Approximation
policy function approximation 也叫policy gradient
之前的方法都是value based ,本次的算法是policy based
在这之前的策略都是用表格来表达的: 即给定$(s_i,a_j)$ ,会得到一个策略$\pi(a_i|s_j)$ 。
我们将他写成函数
这里的$\theta$ 是一个向量,表示参数。
用函数代替表格的好处:
- 如果state有很多很多个,那么在存储上会很费力,
- 难以进行泛化,在表格中,如果要更改$\pi(a|s)$,那么一定要访问$\pi(a|s)$ ,而如果用表达式来表达的话,则可以通过更改参数来更改一系列的$\pi$
tabular 和function representations的区别:
定义最优的策略:
在表格情况下,策略$\pi$ 当在每一个state value上都最大的时候是最优的。
在函数表示中,策略$\pi$ 当能够最大化scalar metrics的时候是最优的
怎么获取一个action的probability?
在表格中,使用索引来得到一个action的probability。
在函数中,需要放入神经网络中进行计算得出。
如何更新policies?
在表格中:直接改变表格中的$\pi(a|s)$ 的值
在函数中,通过更改$\theta$ 间接修改策略。
policy gradient的目标函数(metric)是:最大化 $J(\theta)$
policy gradient的两个metrics
metric(度量)
- 第一个metric是state value的加权平均。
在这里$\sum{s \in S} d(s) = 1$ ,既可以代表权重,可以代表选择$v\pi(s)$ 的概率。
如何选择d(s)?
第一种情况是d和$\pi$ 无关。
那么求$\overline v_\pi$ 的梯度不需要得到d对$\pi$ 的梯度。
例如令$d_0(s) = \frac{1}{|S|}$ ,得到均匀分布。
- 或者我们对其中的某些状态很关心$d0(s_0) = 1,d_0(s \not = s_0) = 0$ ,这时候$\overline v\pi = v_\pi(s_0)$
第二种情况是d和$\pi$有关,即d依赖于$\pi$
- 一种基本的情况是$d\pi $满足$d^T\pi P\pi = d^T\pi$
- 那么会有些状态访问的次数较多,有些状态访问的次数较少。
- 第二个metric是average one-step reward
在这里$S \sim d_\pi$ ,有如下公式:
代表在一个状态得到的reward的加权平均。
下面给出average one-step reward的第二种形式:
假设根据一个给定的策略生成了一个trajectory,并有着$(R{t+1},R{t+2},R_{t+3},…)$ 的reward。
那么在这个trajectory中,平均的single-step reward是
注意到最后当$n \to \infty$ 时,可以将$S_t=s_0$ 省去,因为当走了无穷步的时候,从哪一步开始就已经无所谓了。
注意点1:
所有这些的metrics都是$\pi$ 的函数。因为$\pi$ 是由参数$\theta$ 决定,这些metrics也是关于$\theta$ 的函数,也就是说不同的$\theta$ 会产生不同的metric values. 我们就可以找到最优的$\theta$ 来使得这些metrics最优。
注意点2:
这些metrics可以被定义为有折旧的情况(discounted case),即$\gamma \in [0,1)$ ,也可以是undiscounted case的,即$\gamma = 1$
注意点3:
在直观上,$\overline r\pi$和 $\overline v\pi$ 相比,似乎更加”近视“,因为他更多地考虑立即的reward,而$\overline v_\pi$ 考虑整个过程的reward。
实则不然,两个metrics实际上是相互等价的。当$\gamma < 1$ ,有如下公式:
metric还有一种常见的表示形式如下:
它实际上和$\overline v_\pi$ 是相同的,下面给出推导过程:
目标函数的梯度计算
梯度如下:
又可以写作
写成期望的形式便于我们用采样来模拟期望。
下面是推导期望公式的过程:
由链式法则得:
把式子带入梯度表达式中:
因为我们求了$ln(\pi(a|s,\theta))$ 所以我们的$\pi$必须满足$\pi(a|s,\theta) > 0$ ,可以用softmax方式来将$(-\infty ,\infty)$ 的值域归一化到$(0,1)$
同时还满足$\sum_{i=1}^b z_i = 1$
REINFORCE
reinforce是一种 policy gradient algorithm
根据上一节的目标函数,我们可以得到迭代方程:
但我们知道,期望是很难算的, 我们要用stochastic方式来代替真实的期望。
但我们的$q\pi$ 是不知道的,于是我们可以用$q_t$ 来代替$q\pi$
如何对$q_t$进行采样?
基于蒙德卡罗的方法,即本节的REINFORCE
其他方法
注意一:
如何做采样?
- 如何对S做采样?$S \sim d$ ,经过$\pi$ 下不断迭代得到$d$ ,然后采样得到S。但实际中我们没时间等d趋于平稳再采样。
- 如何对A做采样? $A \sim \pi(A|S,\theta)$ , 根据 在$s_t$ 处的策略$\pi(\theta_t)$ 来对A进行采样。
因此,这个policy gradient 方法是on-policy的。
注意二:
如何理解算法?
我们设定$\beta_t = \frac{q_t(s_t,a_t)}{\pi(a_t|s_t,\theta_t)}$
于是原式变为如下:
于是我们就可以发现,我们是通过改变$\theta$ ,来优化$\pi(a_t|s_t,\theta)$ 的值。
所以我们步长$\alpha \beta_t$ 要足够小才能收敛。
- 当$\betat > 0$ , 那么选择$(s_t,a_t) $ 的可能更大,于是有$\pi(a_t |s_t,\theta{t+1}) > \pi(a_t|s_t,\theta_t)$
- 当$\betat < 0$ ,那么$\pi(a_t|s_t,\theta{t+1}) < \pi(a_t|s_t,\theta_t)$
数学推导如下:
当$\theta_{t+1} - \theta_t$ 足够小时,有
系数$\beta_t$ 能够很好地平衡$exploration$ 和$exploitation$
首先$\beta_t$ 与$q_t(s_t,a_t)$ 成正比。
- 如果$q_t(s_t,a_t)$ 比较大,那么$\beta_t$ 也比较大。
- 因此此时算法倾向于使用更大的值来增强$q_t$ ,也就是exploitation
其次:$\beta_t$ 与$\pi(a_t|s_t,\theta_t)$ 成反比。
如果$\pi(at|s_t,\theta_t)$ 很小,那么$\beta_t$ 很大。下次的$pi(a_t|s_t,\theta{t+1})$更大,就会给出更大的选择概率。
因此算法倾向于概率较低的探索操作。即exploration
REINFORCE算法实现如下;
初始化参数$\pi(a|s,\theta), \gamma \in (0,1) ,\alpha > 0$
目标是最大化$J(\theta)$
对于第k次迭代:
- 选择一个$s0$ ,遵循$\pi(\theta_k)$生成episode ,假设episode是${s_0,a_0,r_1,…,s{T-1},a{T-1},r{T}}$
- 对于每个$t = 0,1,2,.,,,T-1$ 执行3和4:
- value update:$qt(s_t,a_t) = \sum{k=t+1}^T \gamma^{k-t-1}r_k$
- policy update:$\theta{t+1} = \theta_t + \alpha \nabla\theta ln \pi(a_t|s_t,\theta_t)q_t(s_t,a_t)$
第十章 actor-critic 方法
actor-critic本身就是policy gradient
The simplest actor-critic
也称QAC(这里的Q是公式中的q,也就是action value)
policy gradient算法:
这个更新策略的算法就是actor, critic则用来估计$q_t(s_t,a_t)$
如何得到$q_t(s_t,a_t)$ ?
两种方法:
- MC learning:这样结合就得到了REINFORCE算法。
- Temporal-difference learning: actor-critic算法。
优化目标函数$J(\theta)$ ,使其最大化。
对于每个episode的第t步,执行如下:
遵循$\pi(a|st,\theta_t)$ 生成$a_t$ ,得到($r{t+1},s{t+1}$) ,然后遵循$\pi (a|s{t+1},\thetat)$ 生成$a{t+1}$
Critic(value update):
Actor (policy update):
这个算法是on-policy 的。
The simplest actor-critic实际上就是 SARSA + value function approximation
advantage actor-critic
也叫AAC ,A2C
首先我们为policy gradient 引入一个新的baseline(b函数)
为什么引入新的b 函数,等式依然成立?
因为如下公式成立:
详细地说:
引入这个b函数有什么用?
我们说$\nabla_\theta J(\theta) = \mathbb E[X]$
那么我们知道
- $\mathbb E[X]$ 和b(S) 无关。
- X的方差和b有关。
所以我们可以通过设置b函数来减小方差。
设置b函数为如下值时,能使得方差最小:
其中$||\nabla_\theta \ln \pi (A|s,\theta_t)||^2$ 可以被认为是一个权重。
但是这个公式太复杂了。我们一般直接用
$b(s) = \mathbb E{A \sim \pi}[q(s,A)] = v\pi(s)$
把上式带入公式中,我们可以得到gradient-ascent算法:
我们叫$\delta\pi(S,A) = q\pi(S,A) - v_\pi(S)$ 为advantage funciton(优势函数)
$v\pi(S)$ 是某个状态下的action的平均值, 所以$\delta\pi(S,A)$ 描述了当前的action和同状态的其他action相比的优劣。
公式还可以写成下面:
于是我们公式中的$\frac{\delta_t(s_t,a_t) }{\pi(a_t|s_t,\theta_t)}$ 决定了step-size(和第9讲REINFORCE中的$\beta_t$ 一样能够很好地平衡$exploration$ 和$exploitation$
A2C ,或者TD actor-critic 的过程:
目标是寻找最大的$J(\theta)$
在每个episode的第t时刻,我们执行如下:
遵循$\pi(a|st,\theta_t)$生成$a_t$ 然后得到$r{t+1},s_{t+1}$
TD error(advantage function):
$\deltat = r{t+1} + \gamma v(s_{t+1},w_t) - v(s_t,w_t)$
Critic (value update):
$w_{t+1} = w_t + \alpha_w \delta_t \nabla_w v(s_t,w_t)$
Actor(plicy update):
$\theta{t+1} = \theta_t + \alpha\theta \deltat \nabla\theta \ln \pi (a_t|s_t,\theta_t)$
这是一个on-policy 的。
off-policy actor-critic
Policy gradient是on-policy的原因是梯度必须服从$\pi$ 策略,这里的$\pi$ 既是behavior policy ,同时这个$\pi$ 也是我们要更新的target policy。
可以使用importance sampling 来把on-policy转为off-policy。
于是我们就可以通过$p1$ 进行采样,然后估计$p_0$ 采样下的均值。 那么热和计算$ \mathbb E{X\sim p_1} [f(X)]$ ?
令f为如下函数:
那么就有
所以$\overline f$ (f的平均数)就可以用来估计$\mathbb E{X \sim p_1}[\overline f] = \mathbb E {X \sim p_0} [X] $
这里的$\frac{p_0(x_i)}{p_1(x_i) }$ 可以被认为是权重,那么直观地看就是对于$p_0$ 相对难取的样本,赋予更高的权重。
这个权重叫做 importance权重。
就是因为我们只能知道$p0(x)$ ,但求不出$\mathbb E{X \sim o_0}[X]$ , 所以才需要importance sampling。
假设$\beta$ 是behavior policy生成的经验采样。
我们的目标是更新target policy $\pi$ 来最大化$J(\theta)$
他的梯度如下:
这里的$\beta$ 是behavior policy ,$\rho$ 是state distribution。
优化:
我们仍然可以通过加上baseline来进行优化:$\delta \pi(S,A) = q\pi(S,A) - v_\pi(S) $ 。
在这之中
于是最终的算法就是
Deterministic actor-critic
DPG和之前的(QAC,A2C、off-policy的actor-critic)相比的一大特点就是他的策略$\pi(a|s,\theta)$ 可以是负数。
于是我们用deterministic policies来解决continuous action(无限个的、连续的action)
之前我们是通过策略 $\pi(a|s,\theta) \in [0,1]$ 来决定要采取哪个动作a。
而现在我们改成下面这样:
意味着我们直接通过s得到a的值,而不是借助每一个action的概率来决定选择哪个a。
$d_0$ 的选择和$\mu$ 无关。
选择$d_0$的两种特殊的情况:
- $d_0(s_0) - 1$ ,$d_0(s \not = s_0) = 0$ . 在这里$s_0$ 是一个特殊的开始状态。
- $d_0$ 取决于behavior policy 在$\mu$ 上的内容。
这里面的梯度没有action A。
所以这个deterministic policy gradient 是一个off-policy的方法。(因为我们不需要关心这个a是通过哪个策略得到的)
梯度上升:
注意:
$\beta$ 和$\mu$ 是不同的。
$\beta$ 也可以设置为$\mu + noise$.
如何选取$q(s,a,w)$ ?
- 线性函数: $q(s,a,w) = \phi^T(s,a)w$
- 神经网络:DDPG