题目链接 - Codeforces Round 933 (Div. 3)

博客中的代码仅供参考，请勿直接提交源代码，这对提升实力毫无作用!!!

题目写一半，自己不小心把编译器搞坏了，中途又重新下载mingw呜呜呜,好在这场时间长

A. Rudolf and the Ticket

题意

有两个数组a和b，长度分别为n，m。即$a_1,a_2,…,a_n,b_1,b_2,..,b_m$ 。

现要求你从两个数组中各选择一个数$a_i,b_j$ 并且要求$a_i + b_j \le k$ ,问有多少种选法。

思路

二分查找， 对b数组排序，然后枚举$a_i$ , 使用upperbound来在b中查找第一个大于$k - a_i$ 的下标p，那么b数组中的区间$[0,p-1]$上的数都满足和$a_i$ 相加之后小于等于$k$。 于是产生了$p$的贡献。按此理计算出总贡献即可。复杂度$O(nlogn)$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
void solve(){
    int n,m,k;
    cin>>n>>m>>k;
    vector<int> a,b;
    rep(i,1,n){
        int num;cin>>num; a.push_back(num);
    }
    rep(i,1,m){
        int num;cin>>num; b.push_back(num);
    }
    int sum = 0;
    sort(b.begin(),b.end());
    for(auto p : a){
        int t = k - p;
        sum += upper_bound(b.begin(),b.end(),t) - b.begin();
    }
    cout<<sum<<endl;
}
signed main(){
    int T = 1;
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

B - Rudolf and 121

题意

现在有一个长度为$n$的数组$a$，$a_1,a_2,…,a_n$ 要求你使用任意次如下操作，问能否使得数组a全为0 。

选择一个下标$i(2 \le i \le n-1)$，然后进行下面三步：

  1. 令$a_{i-1} -= 1$
  2. 令$a_{i} -= 2$
  3. 令$a_{i+1} -= 1$

思路

贪心，观察操作可以发现，我们若想让$a_1$ 归零， 那么就必须选择$i = 2$ 进行操作，并且要准确地操作$a_1$ 次。 此时$a_1$就一定变为了0 。更新数组,即更新$a_1,a_2,a_3$ 。

然后我们就按照此法再令$i = 3$ ，进行$a_2$次操作，来试图将$a_2$ 归零。 但我们发现如果某个数变成了负数，那么他永远无法变成0，因此我们就可以输出NO并结束这组样例。

如此法遍历整个数组即可。

在遍历完整个数组后，我们还无法得知$a_{n-1}, a_n$ 是否成功清零，判断一下即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
void solve(){
    int n;
    cin>>n;
    vector<int> vec(n+5);
    rep(i,1,n) cin>>vec[i];
    rep(i,2,n-1){
        if(vec[i-1]<0||vec[i]<0||vec[i+1]<0){cout<<"No\n";return ;}//如果某个数变成了负数
        if(vec[i-1] == 0) continue;
        int t = vec[i-1];//要进行的操作次数
        vec[i] -= 2 * t;
        vec[i+1] -= t;
        vec[i-1] -= t;
    }
    if(vec[n-1] != 0 || vec[n]!=0){cout<<"No\n";return ;}//如果这两个数没有成功清零
    cout<<"Yes\n";
}
signed main(){
    int T = 1;
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

C - Rudolf and the Ugly String

题意

如果一个字符串中存在子串map 或者 pie ，那么就说这个子串是丑陋的，否则就说它是美丽的。现在给你一个字符串，问最少需要删除几个字符才能使得字符串是美丽的。

思路

我们需要拆散这个字符串中的map 和 pie ， 容易发现，如果存在某个子串是map ，那么我们删除中间的a即可，这样能够删除这里的map，并且保证不会出现新的map ,pie也是同理， 因此我们找这个字符串中存在几个map或者pie子串即可（吗？）

如果仅仅想到这一步，那么你将获得一发罚时。因为如果字符串中存在子串mapie,那么我们照此法将会删除a和i两个字符，然而直接删除p字符就可以同时拆散map和pie 。

所以最终答案应为字符串中map与pie的数量相加再减去mapie的数量

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
void solve(){
    int n;
    cin>>n;
    string str;
    cin>>str;
    int ans = 0;
    for(int i = 0;i<n-2;i++){
        if(i<=n-5 && str.substr(i,5) == "mapie"){ans--;} //每出现一个mapie就让答案减一
        if(str.substr(i,3) == "map") ans++;
        if(str.substr(i,3) == "pie") ans++;
    }
    cout<<ans<<endl;
}
signed main(){
    int T = 1;
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

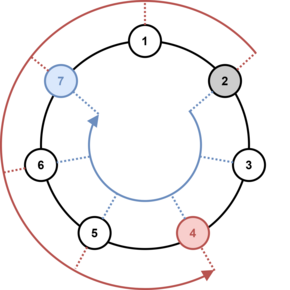
D. Rudolf and the Ball Game

题意

有n个人按顺时针顺序s围成一个环，标号分别为$1,2,..,n$ , 如图：

起初球在第x个人的手中，下面进行m次传球。每次传球遵循如下格式：r c 其中r为一个整数，表示传球的距离。c为0 1 ? 中的一个字符 , 0表示下一步要顺时针传球， 1表示这次传球是逆时针的，?则表示这次传球不确定是顺时针还是逆时针。如上图中2号人顺时针传距离5时，传给了7，逆时针时则传给了4 。

问进行完m次传球后， 哪些人可能拿到球。

思路

dp，我们使用一个数组$dp$记录上一步都哪些人可能获得球后，起初$dp[x] = 1$ ，其他值为0 。

对于每一步传球操作，根据操作情况来生成一个新的数组$f$表示进行完这步操作后哪些人可能会获得球。然后将$f$内容复制给$dp$之后， 清空$f$ 。不断重复如此即可得到最终的数组。

对标号$1,2,…,n$ 的人进行循环取模操作会比较复杂，可以考虑令所有人的标号减一，最终输出的时候通过加一来恢复原始标号。

代码

还有一种存储方式是用set， 但原理相同，这里不在赘述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
void solve(){
    int n,m,x;
    cin>>n>>m>>x;
    //这里的vector就等价于数组，但是支持直接赋值整个数组
    vector<bool> dp(n+5);//老数组
    vector<bool> f(n+5);//新数组
    dp[x-1] = 1; //做了减一操作，更方便取模
    rep(i,1,m){
        int k;char op;
        cin>>k>>op;
        for(int i =0;i<n;i++){
            if(dp[i]){
                if(op !='0') f[(i-k+n)%n] = 1; //1和?会进行逆时针操作
                if(op !='1') f[(i+k)%n] = 1;//0和?会进行顺时针操作
                //算是一个小技巧,可以少写一个判断
            }
        }
        dp = f;//令dp等于f
        fill(f.begin(),f.end(),0);//清空f
    }
    vector<int> ans;//记录哪些人可能获得球
    rep(i,0,n-1) if(dp[i]) ans.push_back(i+1);
    cout<<ans.size()<<'\n';
    for(auto p : ans){
        cout<<p<<" ";
    } 
    puts("");

}
signed main(){
    int T = 1;
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

E. Rudolf and k Bridges

题意

现在有n行m列的网格a，$a_{i,j}$ 表示第$i$行第$j$ 列的海水深度 ， 保证第1列和第m列是大陆， 深度为0。

对每行你可以按照如下规则建桥：

在第$1$列和第$m$列必须要有支柱。然后你可能还需要在海中树立一些柱子。需要保证不存在任何两个相邻的柱子之间的距离大于d，如果两个柱子的距离分别为$i,j$ 那么他们之间的距离是$j - i - 1$ 。

建造一个桥所消耗的费用为 这座桥上所有柱子所在的海水深度加一 的和。

现在需要你建造k个连续的桥。即选择一个$i,i\le n-k+1$，在$i,i+1,…,i+k-1$ 行都建一个桥。问最少需要多少费用。

思路

比较容易得知，对于建造不同的桥，他们的费用是互不影响的。因此我们可以分别计算这n座桥的建造费用，然后选择区间和最小的那组即可。

我们先讲在找到每行的建桥费用并存入ans数组后， 如何找这k个连续的桥（如果你已经会了就跳过）

我们对ans数组进行计算前缀和 ，存入sum中， 于是$sum[i] - sum[i-k]$ 则表示了从第$i-k+1$ 开始建k座桥需要的总花费。于是枚举每一个可能的i，令$res$为所有可能中的最小值即可。

下面来探讨如何计算建造某个桥的费用。

我们可以使用dp的思想， $dp[i]$ 表示在第$i$列立下一根柱子的情况下，建好前$i$格最少需要多少花费，这样$dp[m]$ 就是建造这整座桥的花费。我们$dp[i]$ 必须由$dp[i-1],dp[i-2],…,dp[i-k-1]$ 中的某一个转移而来，可以发现，在建造完成第$i$格的柱子后，不论之前的方案如何，对之后的影响都是相同的。于是我们选择这些元素中值最小的作为母状态即可。

但是如果我们直接枚举$dp[i-1],dp[i-2],…,dp[i-k-1]$ 这些内容，那么计算一个桥的复杂度就是$O(m*d)$ 这显然会导致超时。于是我们考虑使用数据结构来加速。

下面介绍方案一：优先队列

我们使用优先队列存储一个结构体，表示柱子的下标$x$以及$dp[x]$ , 并且规定队头元素是$dp[x]$最小的那个，这样我们就保证可以在O(1)的时间内选出值最小的那个元素。 同时我们每次使用队头元素前都要检查队头元素是否过期（若队头元素的下标$x$与当前下标$i$ 的距离超过了d ,那么它就已经过期，在之后都无法使用），如果过期，就直接出队。

通过上面的构造，我们的优先队列就满足了如下两个性质：

  1. 队头元素一定是花费最小的那个。
  2. 队头元素一定没有过期

于是我们就可以借此来知晓$dp[i]$的值，即$dp[i] = pq.front().was + dep+1$ 。 其中$was$表示花费，$dep$表示第$i$格的深度。之后将$(i,dp[i])$入队。 复杂度为$O(mlogm)$

方案二： 单调队列

很常用的一个数据结构。我们使用一个双端队列，并维护这个队列是递增的。和上面的优先队列原理类似。我们保证队头元素一定不是过期的，如果已经过期就出队它。（若下标$x$和$i$的距离大于$d$，那么我们说$x$已经过期了），同时在入队时，我们保证入队的这个元素一定比队尾元素更大，如果违背了这个规则，我们就不断从队尾出队（这是一个双端队列，所以可以从队尾出队），等到不违背这个规则时，再入队元素。

于是我们的队列就满足了如下两个性质：

  1. 队列中的所有元素从队头到队尾单调递增，因此队头元素一定最小
  2. 队列中队头元素一定不是过期的。

于是我们就可以保证得到正确的$dp[i]$ ，于是就可以得到一个桥的花费，即$dp[m]$

代码

优先队列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
struct Node
{
    int x; //下标x
    int wast;//花费waste
    friend bool operator<(Node n1,Node n2){ //用来决定优先队列的排序顺序
        return n1.wast > n2.wast;
    }
};

void solve(){
    int n,m,k,d;
    cin>>n>>m>>k>>d;
    vector<int> ans;
    ans.push_back(0);
    int t = n;//n还有用
    while(t--){//计算这n行各自的花费
        priority_queue<Node> pq;
        int x;cin>>x;pq.push({1,1});//第一个一定是0,所以直接入队{1,1}
        for(int i = 2;i<=m;i++){
            cin>>x;
            while(pq.top().x+d+1<i){//不断出队过期元素
                pq.pop();
            }
            if(i == m){//如果到达了河对岸
                ans.push_back(pq.top().wast+x+1);//可以存答案了
                break;
            }
            pq.push({i,pq.top().wast+x+1});//入队元素
        }
    }
    for(int i = 1;i<=n;i++){
        ans[i] += ans[i-1];
    }
    int res = INF;
    for(int i =k;i<=n;i++){
        res = min(res,ans[i] - ans[i-k]);
    }
    cout<<res<<endl;
}
signed main(){
    int T = 1;
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

单调队列(代码来自队友)：

这是队友CSDN主页，超强！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <cstdio>
#include <vector>
#include <set>
#include <queue>
#define mk make_pair
using namespace std;
typedef long long ll;
const int maxn=105;
const int maxm=2e5+5;
const ll inf=1e18;

int T,n,m,k,d;
int a[maxm];
ll dp[maxm];

ll cost[maxn];

int main(){
	cin>>T;
	while(T--){
		cin>>n>>m>>k>>d;
		for(int bridge=1;bridge<=n;bridge++){
			for(int i=1;i<=m;i++)cin>>a[i],dp[i]=inf; //初始化dp为全INF(最大值)
			deque<pair<ll,ll> > q;
			dp[1]=1;
			q.push_back(mk(1,1));
			for(int i=2;i<=m;i++){
				dp[i]=min(dp[i],q.front().first+a[i]+1);
				while(!q.empty() && dp[i]<=q.back().first)q.pop_back();//保证队列单调性
				q.push_back(mk(dp[i],i));
				if(i-d>q.front().second)q.pop_front();//保证队头不过期
			}
//			cout<<dp[m]<<endl;
			
			cost[bridge]=cost[bridge-1]+dp[m];//dp[m]是建这座桥的最少费用,cost直接计算了前缀和
		}
		ll ans=inf;
		for(int i=k;i<=n;i++)
			ans=min(ans,cost[i]-cost[i-k]);
		cout<<ans<<endl;
	}
	return 0;
}

F - Rudolf and Imbalance

题意

现在给你三个数组$a,d,f$ , 长度分别为$n，m，k$，你可以从$d$和$f$中各选出一个数 $di, f_j$ 然后把$d_i +f_j$ 放入a中， 问进行最多一次 该操作后， a数组中的 $MAX{i=1}^{n’-1}(a_{i+1} - a_i)$ 最小是多少。 其中的$n’$ 表示为进行至多一次操作之后的a的元素数量。

保证a数组是有序的。

思路

由于我们只能插入一个数，因此只有插入到最大的那个间隙中，才能使得最大间隔变短。 因此我们可以先求出最大间隔$mx$和次大间隔$semx$ , 并找到产生最大间隔的那两个数$l$和$r$，即$r - l = mx$ 。 假设我们找到了一个数$t$，来插入到$l$和$r$中间，那么整个数组a的最大间隔就 变为了 $MAX(semx,abs(t-l),abs(r-t))$ ， 我们设$mid = \frac{l+r}{2}$ ，那么很明显，semx是一个定值，因此我们的t越靠近mid，便越可能得到更小的答案。于是整道题的目标就变为了找到最接近$mid $的那个$t$ 。

我们对数组$f$进行排序， 然后枚举$d$中 的元素$x$， 使用lower_bound来从$f$中找到最接近$mid - x$ 的两个值作为$t$的 待选项，借此更新更优的$t$ ,得到更优的$ans$ 。最终我们再和次大间隔$semx$取$max$即可。

需要注意的是，

  1. 注意lower _bound之后可能找到的是数组边界，此时可能会不存在其中一个待选项$t$。
  2. 要特殊考虑n == 2 时没有次大值$semx$的情况。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
void solve(){
    int n ,m,k;
    cin>>n>>m>>k;
    vector<int> a(n+5);//数组a
    for(int i = 1;i<=n;i++) cin>>a[i];
    int mx = 0,semx = 0;//a中相邻两个数的差，最大和次大
    int l,r;//最大差的左项和右项
    //初始化mx和semx,l,r
    if(n>=3){
        if(a[3]-a[2]>a[2]-a[1]){
            l = a[2],r = a[3];
            mx = a[3]-a[2];
            semx =a[2]-a[1];
        }else {
            l = a[1],r = a[2];
            mx = a[2]-a[1];
            semx =a[3]-a[2];
        }
    }else if(n == 2){
        mx = a[2]-a[1];l = a[1];r = a[2];
    }
    //找mx和semx,l,r
    rep(i,3,n-1){
        if(a[i+1]-a[i]>mx){
            semx = r - l;
            mx = a[i+1]-a[i];
            r = a[i+1],l = a[i];
        }else if(a[i+1]-a[i]>semx){
            semx = a[i+1]-a[i];
        }
    }
    int mid = (l+r)/2;
    vector<int> d,f;
    rep(i,1,m){int num;cin>>num;d.push_back(num);}
    rep(i,1,k){int num;cin>>num;f.push_back(num);}
    sort(f.begin(),f.end());
    int ans = INF;
    for(auto x : d){//枚举d
        int p = upper_bound(f.begin(),f.end(),mid-x) - f.begin();
        if(p!=k){
            int t = f[p]+x;
            int newans = max(abs(l-t),abs(t-r));
            ans = min(ans,newans);
        }if(p!=0){
            int t = f[p-1]+x;
            int newans = max(abs(l-t),abs(t-r));
            ans = min(ans,newans);
        }
    }
    if(ans > mx){cout<<mx<<endl;return;}
    cout<<max(semx,ans)<<endl;
}
signed main(){
    int T = 1;
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}