题目链接

A. Turtle Puzzle: Rearrange and Negate

题意

有一个长度为n的数组a，进行两步操作，第一步重新排列数组内元素的顺序， 第二部选择一个连续区间，将其中的元素取反。问进行完这两步操作后，数组元素的值的总和 最大是多少。

思路

很显然，把所有的负数放到一起，然后把这段区间取反即可。答案就是所有数的绝对值的和。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define int long long
#define rep(i,l,r) for(int i = l;i<=r;i++)
#define per(i,r,l) for(int i = r;i>=l;i--)
const int INF = 0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> PII;
void solve(){
  int n;
  cin>>n;
  int ans = 0;
  for(int i =1;i<=n;i++){
    int num;cin>>num;
    ans += abs(num);
  }
  cout<<ans<<'\n';
}
signed main(){
  int T = 1;
  cin>>T;
  while(T--){
    solve();
  }
  return 0;
}

B - Turtle Math: Fast Three Task

题意

给n个数， 每次你可以选择如下操作之一 ，

  • 删除一个数
  • 使一个数的值加一

问最少需要几步可以使得所有数的总和是3的倍数。

思路

我们考虑不进行操作时的总和，

  1. 总和本身就是3的倍数，不需要操作，直接输出0
  2. 总和除以3之后余2， 对任意数进行加一操作即可，输出1 。
  3. 总和除以3之后余1， 那么有两种选择，一是 删除一个“除以3余1的数” ，二是进行两次加一操作。因此可以记录一下是否存在“除以3余1的数” ，如果存在就输出1，不存在就输出2

代码

$solve$ 函数之外的代码与A题相同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void solve(){
  int n;
  cin>>n;
  int cnt1 = 0;//除以3余1的数的数量
  int sum = 0;
  rep(i,1,n){
    int num;cin>>num;
    if(num%3 == 1) cnt1++;
    sum += num;
  }
  if(sum%3 == 0){cout<<0<<'\n';return;}
  if(sum%3 == 2){cout<<1<<'\n';return;}
  if(sum%3 == 1){
    if(cnt1)cout<<1<<'\n';
    else cout<<2<<'\n'; 
    return ;
  }
}

C. Turtle Fingers: Count the Values of k

题意

给出 $a , b, l$ , 那么有$l = k a^x b ^ y$ ,问$k$有几种可能。

如 $a = 2, b= 5,l = 20$ ，那么可以选择

  • $k = 1,x = 2,y = 1$
  • $k = 2,x = 1,y = 1$
  • $k = 4,x = 0,y = 1$
  • $k = 5,x = 2,y = 0$
  • $k = 10,x = 1,y = 0$
  • $k = 20,x = 0,y = 0$

共六种可能 。

思路

暴力枚举即可。需要检查当$a^x$ （或者$b^y$）不再是$l$的因子时，及时break。 以及在枚举过程中可能出现重复的k，使用set去重即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void solve(){
  int a,b,l;
  cin>>a>>b>>l;
  set<int> ans;
  for(int ax = 1;ax<=l;ax*=a){//a的x次方
    if(l%ax) break;
    for(int by = 1;by<=l;by*=b){//b的y次方
      if(l%by) break; 
      if(l%(ax*by)) break; //如果不存在这样的整数k，就break
      ans.insert(l/ax/by);
    }
  }
  cout<<ans.size()<<'\n';
}

D. Turtle Tenacity: Continual Mods

题意

给出数组$a_1,a_2,…,a_n$ 判断是否可能存在重排后的数组b， 使得$b_1\ mod \ b_2 \ mod \ …\ mod\ b_n \not= 0$。

思路

我们先找到最小的数$mn = MIN_{i=1}^n a_i$

如果a数组中只有一个$mn$， 那么我们考虑把$mn$排在最前面，这样每次取模后得到的结果都是$mn$，最终的答案也就是$mn$，一定不为0。

考虑如果有多个mn，那么我们必须用另一个数 $num(num \in a)$ 来取模 $mn$, 从而得到一个比mn更小的数$t = num \ mod\ mn$， 借此t 变成了新的最小的数，并且一定唯一。

因此只要存在一个数，他不是mn的倍数，我们就可以让他作为num，这样就可以使得t不为0 ，最终使得答案是t。

总的来说，决策思路为：如果最小数$mn$的数量大于1，并且不存在$num$使得$num$不是$mn$的倍数，就无解，其他情况均有解。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void solve(){ 
	int n;
	cin>>n;
	vector<int> a(n+5);
	int mn = INF;
	rep(i,1,n) {cin>>a[i];mn = min(mn,a[i]);}
	bool flag = 0;
	rep(i,1,n){if(a[i]%mn != 0) flag = 1;}
	int cnt = 0;
	rep(i,1,n){if(a[i] == mn) cnt++;}
	if(flag == 0 && cnt>=2){
		cout<<"NO\n";
	}else cout<<"YES\n";
}

E - Turtle vs. Rabbit Race: Optimal Trainings

题意

给出n个区间，他们从左到右并列相接。长度分别为$a1,a_2,…,a_n$ ， 现在你会选择其中相邻的几个区间， 假设为第$l$ 个到 第$r$ 个区间， 那么你就相当于要学习$\sum {i=l}^r a_i$ 天， 第一天你的分数增加u， 第二天增加u-1, … , 第$i$ 天增加 $u -i + 1$ , 如果你学的天数过多，可能在某一天增加的分数为负数。

接下来有多组询问， 每次给出 $l$和$u$ ,你需要找到一个r， 使得你得到的总分数最大。 如果存在多个r 使得分数最大， 那么输出最小的r。

思路

我们可以发现，当学习u天过后， 再学习会减少总分数。 我们维护一个前缀和数组sum， 那么我们只需要找到一个r，使得$sum[r]-sum[l]$ 与 $u$的差的绝对值尽可能小 。 而由于a是正整数， 因此$sum$数组是单调递增的，我们在sum数组中使用二分查找位于$sum[l]+u$ 附近的两个位置，然后选出其中更靠近u的即可。

代码

注意使用$lowber_bound$寻找的r下标可能会超出n，应该取$r = min(r,n)$

找出的最终的r可能会比l要小（因为进行了r - 1操作） ， 因此最终还要取$r = max(r,l)$

可以计算出两个r的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void solve(){
	int n;
	cin>>n;
	vector<int> a(n+5);
	vector<int> sum(n+5);
	rep(i,1,n) cin>>a[i];
	rep(i,1,n) sum[i] = sum[i-1] + a[i];
	int q;
	cin>>q;
	while(q--){
		int l,u;
		cin>>l>>u;
		int r = lower_bound(sum.begin(),sum.begin()+1+n,sum[l-1]+u) - sum.begin();
		r = min(r,n);
		int cnt1 = sum[r] - sum[l-1];
		int cnt2 = sum[r-1] - sum[l-1];
		int score1 = (u + u-cnt1)*cnt1 / 2;
		int score2 = (u + u-cnt2)*cnt2 / 2;
		if(score2 > score1) r--;
		r = max(r,l);
		cout<<r<<' ';
	}
	puts("");
}

F - Turtle Mission: Robot and the Earthquake

题意

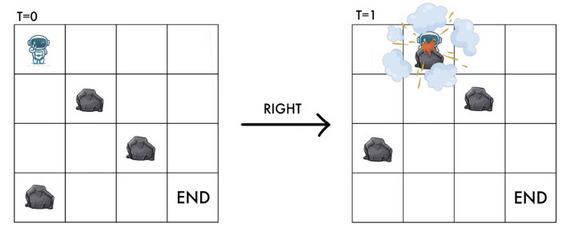
在一个nm的地图中， 你最初位于$(0,0)$处，你需要到达地图的右下角$(n-1,m-1)$ 。但是地图上会有一些石头， 他们每单位时间都会向上循环移动一格，（*循环移动指的是当移动出地图边界时，会出现在地图的另一侧）

保证最右边一列不存在石头。

你每次可以选择向 上，下，右三个方向移动。其中上下方向为循环移动。

如果你向下移动，那么由于石头在向上移动， 如果你的下方两格中存在石头，你就会撞上石头。

move1

同样，如果你向右移动，并且右下方有石头，也会撞上石头

问能否到达终点，如果能就输出最小步数，不能则输出-1

思路

机器人到达最后一列后，没有了石头，就很好办了。所以我们重点考虑机器人如何最快地到达最后一列。

由于每次石头都向上移动， 并且机器人和石头都是循环移动，因此我们可以认为石头不动，而机器人向下移动。这样机器人本身的向下移动就变成了向下移动两格，机器人的向右移动变成了向右下移动。

由此，我们就将本题的重点转化为了终点为最右一列的任意一点，起点为(0,0) 的广度优先搜索 。 于是我们使用队列来找到最少步数，以及此时的坐标（相对石头的坐标）。由于终点不会像石头那样不断向上移动， 因此每走一步，终点都相对于石头向下移动了一格 。

此时我们可以得到当前位置相对于石头的坐标为$(x,m-1)$ ，总共走了$step$步， 此时终点位于$((n-1+step)\ mod \ n,m-1)$ 。

设此时终点的横坐标为$pos$,即 $pos = (n-1+step)\ mod \ n$ 。这时我们可以选择两种方法到达终点，直接到达，花费$abs(x-pos)$时间， 或者穿越边界再到达终点，花费$n-abs(x-pos)$ 。二者取min即可。

代码

需要注意，不能像普通的$bfs$走迷宫一样，直接将墙壁位置的$vis$设置为$1$来省去mp数组：

考虑循在同一列循环的情况， 可能发生如下情况：现在位于$(3,1)$ ，下一步是$(3,3)$ ，并且在上一次循环时已经走过了$(3,2)$ 。那么此时$vis[3][2]$ 等于1 ，并且可以到达。
而$vis[3][2]=1$还有一种可能是$(3,2)$处有一个石头，那么反而又不能到达。因此我们的$vis[3][2]=1$ 出现了两种不同的结果，这是不被允许的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
int mp[1005][1005];
int vis[1005][1005];
struct Node{
    int x,y;
    int step;
};
void solve(){
    int n,m;
    cin>>n>>m;
    rep(i,0,n) rep(j,0,m){mp[i][j] = vis[i][j]=0;}
    queue<Node> q;
    rep(i,0,n-1) rep(j,0,m-1) cin>>mp[i][j];
    q.push({0,0,0});
    vis[0][0] = 1;
    while(q.size()){
        int x = q.front().x;
        int y = q.front().y;
        int step = q.front().step;
        if(y == m-1) break;
        q.pop();
        int xx = (x+1)%n,yy = y + 1; //xx表示向下移动一格时的坐标，yy则是向右移动一格
        if(mp[xx][yy]==0) {
            if(vis[xx][yy]==0){
                q.push({xx,yy,step+1});
                vis[xx][yy] = 1;
            }
        }
        int xx2 = (x+2)%n;//xx2表示向下移动两格时的坐标
        if(mp[xx][y]==0&&mp[xx2][y]==0){
            if(vis[xx2][y]==0){
                q.push({xx2,y,step+1});
                vis[xx2][y] = 1;
            }
                
        }
    }
    if(q.empty()) {cout<<-1<<'\n';return ;}
    int step = q.front().step;
    int x = q.front().x;
    int pos = (n-1+step)%n;
    int ans = step + min(abs(pos-x),n-abs(pos-x));
    cout<<ans<<'\n';
}